Making Mathematics: Probabilistic Number Theory Project Teaching Notes

Home > Mathematics Projects > Probabilistic Number Theory > Teaching Notes

Teaching Notes for the
Probabilistic Number Theory Problem

If you want to carry it to completion, this project will require a fair amount of teaching. Think of it in five phases:

Introduction: what are the problems asking?
Perfect squares: a complete solution.
Empirical investigations: running simulations.
Mathematizing: translating to infinite products and sums.
Analysis: evaluating the products and sums.

Students can get a good research experience by carrying out the first three items; the last two are rather advanced and will stretch your best students. In addition, some students will want to take a detour to look at things like the fundamental theorem of arithmetic--the fact that every integer can be factored in essentially one way into a product of primes. This is discussed on The Fundamental Theorem of Arithmetic.

So, there are many ways to do this. Here’s just one possibility.

Phase 1.

What does probability look like in infinite sample spaces? Discuss the difference between “probability 0” and “impossible” (see Results). Work through some “dartboard” examples of geometric probability. This could take two or three classes. Then work through the Warm Up Problems. That will take another class. It’s really important at this stage to get students talking and writing about their thinking so you can catch the subtle (and inevitable) misconceptions that develop. For example, get them to explain their intuition about the probability of getting “3” on a random pick of integers. Why is this different from “getting 3 if the pick is restricted to the integers between 1 and 100?”

Expect unusual and clever ideas. One (very advanced) student argued that the probability of picking the integer n should be 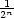. She had two reasons why this was a good choice:

The sum of the probabilities over all the integers is 1.
If someone asks you to pick a number at random, you’re more likely to pick a small number than a very large one, so probability should decrease with size.

Her model led to some very strange consequences.

Phase 2.

Work through the perfect square probability. Ask students to come up with a formula for the number of perfect squares between 1 and n (see Results). After students have ideas that are general in principle, you may have to introduce the greatest integer function and talk a bit about limits. Estimate three classes for this.

Phase 3.

Build and run a simulation. This could take anywhere from a couple days to a couple weeks, depending on how facile your students are with the relevant technology. Try to build the simulation so that the “test” is modular--that is, the same simulation should estimate the probability that an integer is prime or square, just by changing the tester. This is an especially nice project for a computer science class.

If you are using Mathematica, a crude start on a program that lists the primes in a given range goes something like this:
g[n_] := If[PrimeQ[n] == True,1,0]*n

This models a function g defined by

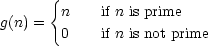{ g(n) = n if n is prime 0 if n is not prime

Then define f that maps g over the integers from 1 to m:

 f[m_] := Map[ g,Range[m]]

So, for example, f(100) outputs a list of 100 numbers that contains all the primes between 1 and 100 (and some zeros).

Phase 4.

Here’s where more direct teaching begins. Building on the Warm Up Problems, you’d like students to reason that the probability that a number between 1 and 100 is prime is

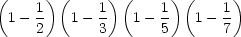( 1)( 1 )( 1)( 1) 1- 2 1- 3 1- 5 1 - 7

This is because a composite number between 1 and 100 has a prime factor between 1 and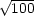

. So, a number between 1 and 100 is prime if and only of it is not divisible by 2, 3, 5, or 7. And you’d like things to generalize from here.

You can expect things like this:

The number of integers not divisible by 2 is half the total. The number not divisible by three is of the total. The number not divisible by four is of the total. The number not divisible by five is of the total. Primes aren’t divisible by any numbers (apart from one and themselves of course). Maybe there’d be a way to work out the proportion of primes through the above? I’m going to have a longer think about that...

A brilliant (but incorrect) idea. But it’s the germ of exactly the right idea, and you’ll have to find a way to tease out the subtle mistake (the 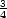). What’s worse is that this brilliant mistake is more than likely not the one that will happen with your students. Think about several classes (maybe a week) to get this solid, and beware that, even then, it won’t be solid for some students.

The point here is to get students comfortable with writing down a mathematical expression that, if evaluated, would give the right probability. So, this phase is as much about building confidence in the technique as it is about developing skill at the technique. For example, the problem above (pick a prime less than 100) can be “checked” in a couple ways: Have one group of students evaluate the product and another count the primes between 1 and 100. Then try the same experiment (using a CAS) with a sample space of 1-500. When you get to the infinite product, you have a real laboratory for experimentation.

You might ask students to compare

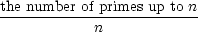the-number-of primes-up-to n- n

with

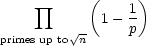( ) prod 1 V~ - 1 - p primes up to n

for some values of n between 1 and 1000. This “product notation” is similar to summation notation. For example,

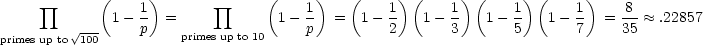prod ( ) prod ( ) ( )( )( )( ) 1 - 1 = 1- 1 = 1 - 1 1 - 1 1- 1 1- 1 = -8 ~~ .22857 primes up to V~ 100 p primes up to 10 p 2 3 5 7 35

Here’s a table of the first 168 primes (the primes up to 1000). It was generated in Mathematica by the command

TableForm[Table[ {n,Prime[n]},{n,1,168}]]

n	the nth prime

1	2

2	3

3	5

4	7

5	11

6	13

7	17

8	19

9	23

10	29

11	31

12	37

13	41

14	43

15	47

16	53

17	59

18	61

19	67

20	71

21	73

22	79

23	83

24	89

25	97

26	101

27	103

28	107

29	109

30	113

31	127

32	131

33	137

34	139

35	149

36	151

37	157

38	163

39	167

40	173

41	179

42	181

n	the nth prime

43	191

44	193

45	197

46	199

47	211

48	223

49	227

50	229

51	233

52	239

53	241

54	251

55	257

56	263

57	269

58	271

59	277

60	281

61	283

62	293

63	307

64	311

65	313

66	317

67	331

68	337

69	347

70	349

71	353

72	359

73	367

74	373

75	379

76	383

77	389

78	397

79	401

80	409

81	419

82	421

83	431

84	433

n	the nth prime

85	439

86	443

87	449

88	457

89	461

90	463

91	467

92	479

93	487

94	491

95	499

96	503

97	509

98	521

99	523

100	541

101	547

102	557

103	563

104	569

105	571

106	577

107	587

108	593

109	599

110	601

111	607

112	613

113	617

114	619

115	631

116	641

117	643

118	647

119	653

120	659

121	661

122	673

123	677

124	683

125	691

126	701

n	the nth prime

127	709

128	719

129	727

130	733

131	739

132	743

133	751

134	757

135	761

136	769

137	773

138	787

139	797

140	809

141	811

142	821

143	823

144	827

145	829

146	839

147	853

148	857

149	859

150	863

151	877

152	881

153	883

154	887

155	907

156	911

157	919

158	929

159	937

160	941

161	947

162	953

163	967

164	971

165	977

166	983

167	991

168	997

Phase 5.

You’re looking at a month or two for this, maybe longer. Study the Results and you’ll see that there’s some very difficult material here. We’ve found it best to move around--introduce something new, then go back and reinforce something from the earlier phases. Paul Goldenberg (a member of the Making Mathematics team) distinguishes between the “clock time” and “calendar time” it takes to understand something. This takes calendar time--slow but steady hammering at the ideas, every day adding a little new territory while and making more permanent structures on what has already been settled.

Translations of mathematical formulas for web display were created by tex4ht.