Teaching Notes for the Patterns in Pascal’s Triangle Problem

Students with a wide range of mathematics backgrounds can work productively on this project. The introductory activities and expectations for student discoveries should differ depending on whether or not students have the useful prerequisites for this project. Depending on the students’ level, you may choose to begin with some of the warm-up problems or use the warm-ups at relevant points during the research (answers to the warm-up problems are available in the results section).

Introducing the Project

For students unfamiliar with Pascal’s triangle, or with any of the settings in which it is encountered, there should be an initial period of exploration with the triangle itself (before launching into its “mod” versions). If time is constrained and you want students to focus on the arithmetic and modular aspects of the problem, introduce them to the triangle by presenting a few rows and the addition rule for generating further rows.

If you are hoping that students will be able to make connections between the different ways of thinking about the entries of Pascal’s triangle, you can have them discover it themselves. Some of the most familiar sources of Pascal’s triangle are given in warm up problem #5. For an algebraic approach to discovering the triangle, ask the students to find, organize, and describe the coefficients of 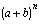for n = 0, 1, 2, etc. This exploration can lead to a discovery of the binomial theorem (warm up problem #6).

A combinatorial approach that you can use with students, with or without an algebra background, is to count the number of different paths that travel from one corner to the opposite corner of an m by n grid in the shortest distance possible (e.g., always heading south or east). The figure below shows the six paths from corner A to corner B of a 2 by 2 grid. Note that a 0 by n “grid” has exactly one possible path. In general, you are moving n + m steps, of which n are in one direction and m are in the perpendicular direction. 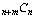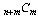Therefore, there are (or ) different ways to choose when to take those n (or m) steps in a particular direction.

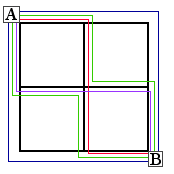
The six paths through a 2 by 2 grid

Another combinatorial problem that generates the triangle is to find the number of distinct n-digit sequences that can be made with k 0’s and n – k 1’s (or vice versa). This setting is particularly powerful because it is a relatively straightforward challenge to turn many different counting problems into a problem involving such sequences. For example, the paths above are just rearrangements of two 0’s and two 1’s with an 0 representing a move south and a 1 representing a move east. For the subset definition in warm up problem #5, the ith digit in an n–digit sequence could indicate whether (1) or not (0) to include the ith element in a set. Showing the equivalence between any two of the settings that generate Pascal’s triangle makes for a good student experience thinking about isomorphisms and explaining connections (download Binomial Handout for another practice activity).

Once students have, either through discovery or presentation, a few rows of the triangle and a means for generating it, ask them to each extend the table by hand for several more rows. There are many patterns in the triangle that students can spend time exploring. They are sure to notice the symmetry of the triangle as well as some of the patterns within the diagonals (those values the same distance from the left, or right, of each row) such as the counting sequence or the triangular numbers (1, 3, 6, 10, 15, …). Some might even notice that the sum of the numbers in each row is a power of 2 (can they explain why?).

Once students have a feel for the triangle itself, introduce some of the main questions (either question 1 alone, 1 with 2, or 1 with 3 would make good starting points).

Working on the Project

Because the values in Pascal’s triangle grow so quickly, an early challenge that students face is the development of an efficient way to extend the rows while keeping track of just the parity of the entries. Once they realize that calculating the numbers becomes unwieldy, encourage them to think of a way to avoid having to make those calculations. Is it possible to keep track of just evenness or oddness (or, in preparation for other moduli, of the remainders after division by 2)? You might suggest that they create an addition table for the possible remainder combinations:

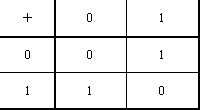
Addition of numbers mod 2

Ask the students to try to prove their arithmetic facts (e.g., that an odd plus an odd is even). If students use the labels “odd” and “even” rather than the remainders, encourage them to use the whole word and not the intitials to avoid later confusion between “O” for “odd” and the remainder 0.

As students move into other divisors, they will probably move from words that describe the remainders (such as “even”) to using the value for the remainder itself. You may choose to introduce the notation and ideas of modular arithmetic at this point or allow them to develop their own descriptions.

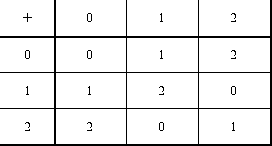
Addition of numbers mod 3

If students propose a table such as the one above, can they prove that their patterns will always hold? For example, if examples suggest that the sum of a number congruent to 2 (mod 3) and one congruent to 1 (mod 3) is always 0 (mod 3), can they prove the general case? One tool they can be shown is the algebraic form for classes of numbers with the same remainder: numbers that leave a remainder, r, after division by d can be represented by dm + r, m an integer (e.g., numbers that leave a remainder of 2 when divided by 3 are of the form 3m +2: 17 = 3^.5 + 2). So the above sum can be represented as (3m + 2) + (3n + 1) = 3m + 3n + 3 = 3(m + n + 1) which is clearly divisible by 3 (and therefore congruent to 0 mod 3).

Once students are ready to begin work on the coloring problems (project problems number 3 or 4), distribute several copies of the Pascal’s triangle coloring sheets for them to use. You might leave questions about alternatives to generating the values in Pascal (rather than the remainders) until this activity, since the coloring may lead some students to think about rules for "adding" colors (red + red = blue, blue + blue = blue, blue + red = red). Once they do so, you can guide them to make a connection to the numerical rules.

It is important to note, at some point, that our interest is not really in the 100th row per se, but in a pattern that we can extend and generalize. “100” is an arbitrary placeholder for “large number that you would not want to work out by hand.” We can use a computer to answer questions such as “how many numbers of a given type show up in row n?” But, the interesting challenge is to find rules that allow us to answer such questions readily for any n, to be able to prove that our rules really work, and to be able to make connections between the formulas that we discover and the different ways that Pascal is generated. That said, technology can be a welcome aid in generating data (especially when we want to look at large portions of the triangle for varying divisors).

Students may struggle to express the patterns that they identify. For example, the number of odds by rows follows a complex pattern that is not easy to explain: 1, 2, 2, 4, 2, 4, 4, 8, 2, 4, 4, 8, 4, 8, 8, 16, 2, 4, 4, 8, …. Students may note that all numbers are powers of two and that each group of four terms is of the form 2ⁿ, 2ⁿ⁺¹, 2ⁿ⁺¹, 2ⁿ⁺², but still find that predicting the next group is not so easy. With enough data, they may notice the way the pattern repeats and extends recursively (see results). Encourage them to express the patterns at first in whatever way they can. Many will be most comfortable with an English sentence or two. Topics which might then be of help (depending on the students’ observations) include binary representations and recursively-defined functions.

Students’ conjectures and questions will head in a number of possible directions. It is appropriate to use those questions as an opportunity to introduce students to topics that might be of help (e.g., number theory ideas, proof by induction).

Thinking in terms of prime and composite numbers is central to understanding the different patterns that arise when coloring the triangle remainders for different divisors. Extension problem #3, which can be proven using the binomial theorem, provides a general purpose tool for analyzing Pascal’s triangle mod a prime number p. The theorem, 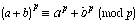, tells us that the pth row will have zeroes in all but the first and last positions because the coefficients of all of the terms in between in the expansion of 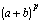are congruent to 0 mod p. To understand this claim, look at the right-hand side of the congruence. None of the 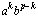terms are present, so their coefficients must be a multiple of p. This congruence can be applied to study the presence of zeroes in other lines. For example, to see what the pattern will be in lines that are a multiple of p, we raise both sides to the kth power:

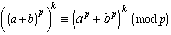and, after expanding,

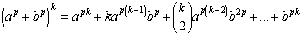
This expansion shows that only every pth entry in row kp will be non-zero.

Using Technology

The resources provide links and pre-made spreadsheets that students can use in their explorations. It is not difficult, however, for students to create their own spreadsheets for exploring Pascal’s triangle.

There are two reasonable approaches to creating a Pascal’s triangle spreadsheet. The easiest route is to make a column and row of 1’s and then fill in all of the other cells with the formula that adds the cell to the left and the cell above (see figure below). These 1’s and formulas do not have to be typed individually. Just type in the contents of cells A1 and B2 and click and drag the contents into the other cells (or use the fill down and fill right commands).

A spreadsheet that generates Pascal’s triangle (rotated 45°)

This spreadsheet design leaves the rows of Pascal’s triangle in the diagonals of the spreadsheet. If students are going to print out and color the sheet, that arrangement poses no difficulty. However, it is also possible to use a spreadsheet to calculate the totals of the entries or the number of odds in a row (using the Sum function). To take advantage of that automated data collection, the triangle needs to have its rows aligned with rows of the spreadsheet. The figures below show how to structure this arrangement. We start the triangle in column C to leave room for summary formulas.

A spreadsheet that generates Pascal’s triangle (skewed)

The output from the above spreadsheet

Students can manually color the cells of the spreadsheet using the paint bucket tool.

Whether students are using a spreadsheet, a program of their own design, or a calculator, the triangle values will ultimately reach a point where the tool is rounding the results of the computations (unless the students use a computer algebra system such as Mathematica®). At this point, the numbers are no longer suitable for determining the remainders. One way to circumvent this limitation is to use the addition rule for generating the triangle and only work with the remainders (e.g., use “= MOD(C1+D1,2)” which adds the two elements above and immediately finds the remainder). This approach would need justification using ideas, such as those discussed above, that show that the remainder of the sum of two numbers can be found from the sum of the remainders of those numbers. Students working with “even” and “odd” might use a formula such as “= If(A1=A2, “E”, “O”)”, but this type of rule becomes cumbersome beyond mod 2.

A good challenge for students who know how to program is to write a program that produces 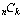mod m even for very large values that the computer cannot handle directly (they can think in terms of the process of calculating 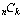and avoid overly large intermediate values).

Closure

All groups should have an answer to the first project question. Their answer should be supported by general reasoning (and not just by number crunching up to the hundredth row). Students may justify their claim using descriptions of, and observing connections between, the numerical and geometric patterns. Students without knowledge of number theory or algebra will have greatest success justifying claims about the geometric patterns. Students should also be able to explain the arithmetic of remainders in a convincing fashion. A younger student may use words or pictures to show why an odd plus an even must be odd, while an older student might do so symbolically.

Each student or group should strive to have a list of main observations, conjectures, numerical results, and, when possible, proofs.