|
Let’s look at a couple strategies for solving the Warm Up Problems. These may
give you some ideas for Trains.
Algorithm 1: A Tree Suppose you’re trying to build all the n-digit numbers that use
only 1s and 2s. The idea is to start with one-digit numbers and build up from there. The
one digit numbers are easy: 1 and 2.
To get the 2-digit numbers, you can either stick a 1 or a 2 onto the end of the existing
one-digit numbers. To get the 3-digit numbers, you can either stick a 1 or a 2 onto the
end of the existing two-digit numbers.
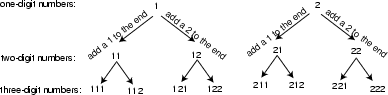
And so on. You can move systematically down this tree. Each time you move to the
left, add a 1 to the end of your number. Each time you move to the right, add a 2 to the
end of your number.
Important things to prove: At any level in the tree, you have all the numbers you
want (there aren’t any missing), and you don’t have any duplications. Also, how does
this algorithm help you find the total number of n-digit numbers using only 1s and
2s?
Algorithm 2: Fill in the Gap Suppose you successfully found all the (n - 1)-digit
numbers that use only 1s and 2s. Now think about an n-digit number. It must start with
either a 1 or a 2, and then it’s followed by an (n - 1)-digit number. If you have a
complete list of those, you’re done.
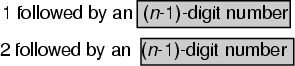

|