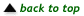The deck of Set. The game of Set is a card game. Each card in the deck has a
picture with four attributes:
- shape: ovals, squiggles, or diamonds
- number: one, two, or three of the selected shape
- color: red, green, or purple
- shading: outlined, striped, or filled
The full deck has one card with each possible combination of attributes. All the cards in
the deck are different. A Set consists of three cards in which each attribute is either
the same on all three cards or is different on each of the three cards. (The word set
has many meanings; to show that we are referring to the meaning defined above, we’ll
capitalize the word.)
The three cards shown above form a Set: all three cards have the same shape and
shading, but the number and color of the shape are different for all three
cards.
These three cards do not form a Set, because the first and the third
cards share the same shading while the card in the middle has a different
shading.
Playing the game of Set. Twelve cards are placed face up on the table. The
players look for Sets. When they find Sets, they put them in their own piles
and put more cards on the table to bring the total number of cards back
to twelve. The game continues until all the cards are dealt and no more
Sets can be found. The player with the most Sets at the end of the game
wins.
Some questions:
- If you pull out 3 cards from the whole deck, what is the probability that
they form a Set?
- If we pull 9 cards from the deck, what is the maximum number of Sets
possible among them?
- How many cards can be left on the table at the end of the game?
- What is the maximum number of cards in a Set-less pile? Can you establish
upper or lower bounds for this maximum?