Extensions for the Amida-kuji Problem
Efficiency: "Worst Case" Assignment
For an amida-kuji with a certain number of players, what
is the maximum number of horizontal lines you would ever
need to create an ordering? If you think of horizontal
lines as having a cost, that number is considered the "worst
case" number. What is the worst case for 2
players?; for 3 players?; for n players?
Sorting Networks
If each horizontal line is thought of as a "sorting
element" that is activated only when the number on the
left is greater than the number on the right, then a "network
lottery" turns into a "sorting network." Computer
scientists have done quite a bit of research on sorting networks. However,
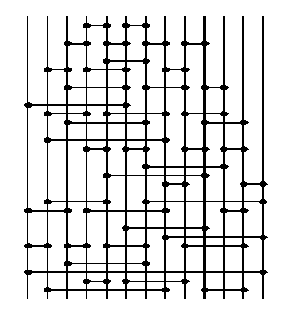
most networks normally allow comparisons between nonadjacent
lines, as in the figure below. It is the most efficient
network that is know for sorting 13 items. The
sorting networks we get from amida-kuji are planar
sorting networks, because the networks can be drawn on
the plane without any lines crossing.
For non-planar sorting networks, see http://unplugged.canterbury.ac.nz/sortnet/index.htm