|





|
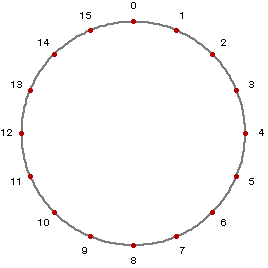
Start with a circle with 16 points, equally spaced:
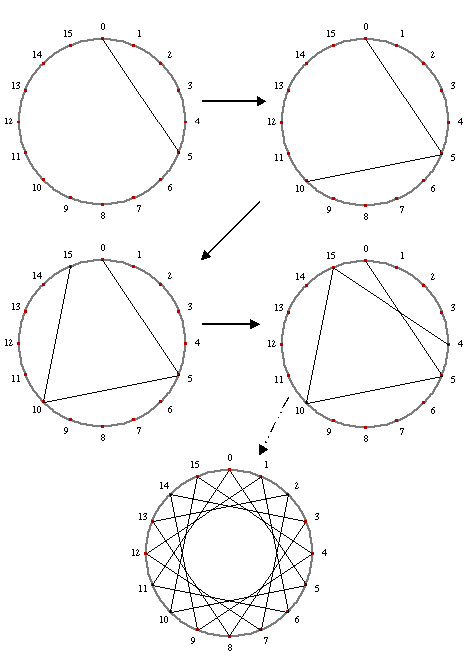
You are going to make a shape by jumping around this circle. Pick a number, j, that determines how far you will move around the circle with each jump. Start at the top point (labeled 0), and draw a segment to the point j steps away. Begin each new jump where the previous one ends and continue this process until one of your jumps returns to the starting point, 0. If, for example, j = 5, you would draw each segment to the point 5 clockwise steps from where the jump began. Each of the first three segments should connect dot numbers that differ by 5, though this is no longer true when you count past 0. Here is what your drawing would look like after 1, 3, 4, and 16 jumps:
Try producing the diagrams for other values of j (e.g., 6, 1, 11). You can print copies of the handout Sixteen Dot Circles to help you with your drawings.
- What happens when you vary the number of dots placed around the circle? Let’s call this number d. Click here to download a set of blank circle diagrams with different numbers of dots, which you can print and use in your investigations.
- What questions can you pose about the shapes produced by connecting the dots? What questions can you ask about the relationships between those shapes, the number of dots around the circle, and the jump sizes?

|