The Connect the Dots setting is an ideal tool for introducing students to the research process. Because the mathematics content is familiar, even older elementary school students will readily produce a wide range of observations and conjectures. Within two class periods, there will be many opportunities for discussions about organizing data, testing conjectures and looking for counterexamples, and writing definitions.
Work on the Connect the Dots setting invariably leads to discoveries involving primes and divisibility, but the nature of a student’s questions plays a large part in determining which ideas will be central to a line of research. For example, one student wanted to know when a figure would have acute or obtuse angles. Her question led her to discover the relationship between the size of arcs and their inscribed angles. Because there is no single question that everyone has to work on, students tend to pose problems at a level of difficulty and sophistication that is appropriate to their background (consider the range of challenges exhibited in the sample student conjectures below).
Student work on the Connect the Dots setting demonstrates why there is no need to choose between developing students’ technical skills and developing their analytical skills (see Research and Technical Content). For younger students, the process of generating examples, seeking patterns, and providing justifications for their conclusions also naturally involves lots of practice in identifying different shapes, skip counting, multiplication, division, and factoring. This practice is in the service of a task that is quite motivating, and the practiced skills are therefore that much more memorable.
DAY 1
Materials:
- Many copies of each page of the circle handouts (you’ll need fewer copies of the circles that have fewer dots)
- A folder for each student or working group to store their circle diagrams and log notes.
- Large paper or oaktag sheets on the wall (for keeping track of student comments during the multi-day investigation)
Distribute copies of the Sixteen Dot Circles handout and explain the rules for drawing figures. You may want to demonstrate by drawing a sample figure on the board. Have everyone make a diagram using the same jump size and then compare their drawings with their neighbor. Then have them each pick their own jump size and make a new drawing. For older students, you may want to omit the rule that the drawing ends when they return to zero. Without this rule, students will have to observe that the drawings repeat their jumps and will have to come up with a question or conjecture regarding the inevitability of figures eventually returning to their starting points (see the discussion of the formula for the number of trips a figure completes around the circle).
While students are working on their drawings, circulate through the class, checking to make sure that, within a given diagram, the jumps are always the same (a drawing is usually in error if a shape looks asymmetrical). Make sure that students are not jumping j + 1 spaces by jumping past j dots. Look to see if they always start their jumps from where the previous jump ended. Once it is clear that students have mastered the mechanics of the process, you should encourage them to experiment further with the current circles or, if they want, with circles with different numbers of dots.
As the students experiment, listen for initial observations and questions. For example, a student might note, "My shape did not hit all of the dots this time" or "I got the same shape as you, but I used a different jump size." Record what you overhear on the board. After students have spent some time experimenting with different values of j and d, bring the class together for a preliminary discussion. Post sheets for each of the following categories of student contributions: questions, observations, conjectures, and definitions (see Mathematical Statements in Introductory Explorations for a further discussion). Then choose one of the comments you overheard, such as the first one above, and ask students under what category they think this comment would fall. Confirm that the statement is an
observation: some shapes hit all of the dots and some do not. Record this observation on the Observation sheet and ask the class what possible questions this observation inspires. Do not expect an immediate answer—allow for a lengthy silence. Here are some possible questions students might suggest:
- Why doesn’t the shape hit all of the dots?
- For which combinations of j and d will a shape hit all of the dots?
- Are there other possible ways to miss some of the dots?
The questions should be added to the Question sheet so that students can refer back to the ideas that are guiding their inquiry each day. You may want to point out that the first question asking why something happened is an easy but important one to pose.
Encourage the students to choose an observation and look for more examples related to it. For example, can they find other pairs of congruent shapes that are generated using different values for j and d? Once students see a pattern in their examples, ask them to write it as a conjecture. A conjecture generalizes their observation to a larger class of drawings. For example, "You will always hit all of the dots when your jump size is 1" is a claim that involves an infinite number of circles with different dot numbers. When you add conjectures to the Conjecture sheet, name them after their creators (e.g., Manya’s Prime Circle Conjecture). Although you are recording a sample of the students’ ideas, each student or working group should also document their efforts and comments in a research log.
Younger students tend to focus initially on which shapes they can make. They will try to make various regular polygons and will note the appearance of "stars." They may ask if it is possible to make a square or a non-square rectangle (you might ask older students about other categories of quadrilaterals and polygons). These types of questions often inspire students to explore a variation of the Connect the Dots problem using sequences of jumps (first 2, then 3, then 2, then 3, etc.). Efforts to make a square when the number of dots is not divisible by four have led to the introduction of non-integral jumps.
DAY 2
Materials: If available, a class set of calculators with the
Connect program or a lab of computers with Internet connections
(see Resources).
During the first day of research, students had time to explore different circle and jump sizes and to record some observations and questions. You can help the class broaden the range of questions that they consider by asking them to identify any numerical variables associated with the setting. A numerical variable in this case might be anything they can count or add as they create a shape or study the final diagram. It could also be a ratio, such as the fraction of dots hit by a shape. In the past, students have identified the following variables:
- The length of the figure (the total jump distance traveled)
- The number of times they moved around the circle to complete the shape
- The number of jumps required to complete the shape
- The number of regions made in each diagram (e.g., a 5-dot circle with a jump size of 2 makes 11 regions)
- Which dots were hit (e.g., when is Dot 1 hit and when is it not?)
Once there are several possible avenues of exploration, students should choose one particular variable or question to study. They should then proceed more systematically and produce an organized list of examples with a sequence of jump sizes or dot numbers. Suggest that they vary one of these variables while holding the other constant. They can also, as one student did, vary both values but hold them in constant proportion to one another (e.g., see what happens when d is always 2.5 times j). Alternatively, they can make a table of examples and vary both variables (one per axis of the table).
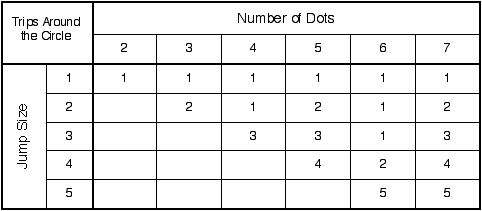
The table below is part of one group’s study of the number of trips around the circle needed to make a shape. The number of trips is a count of the number of jumps that went past or landed on Dot 0 (for example, the shape with 16 dots and a jump size of 5 is completed after 5 trips). The group tried all whole number combinations of j and d up to 15. Obviously, technology can help with such large-scale data collection. Once students have a strong tactile sense of the process, they can be encouraged to use a computer to speed up their work.
DAYS 3, 4, . . .
After the initial explorations are over, research on a problem may proceed in a number of directions and at varying speeds. The range of difficulty of the questions makes it possible for each student to begin work at a level appropriate to his or her skills. The question, "Which combinations of j and d make regular pentagons?" will be trivial for most high school students, but not for all elementary school students. Determining a formula for the number of regions in each diagram is a challenge at any age. Such flexibility is one of the benefits of beginning with a setting rather than a specific question.
As work proceeds, students should be encouraged at the appropriate times to introduce helpful notations and clarifying definitions. For example, function notation can facilitate the statement and justification of many conjectures. If students are studying the resulting shapes, those results can be named S(d, j). Using this notation, one can state conjectures, such as, "S(d, j) = S(d, d – j)" or "S(d, d/4) is always a square." Some students have an easier time generating these symbolic claims than they do writing the comparable, lengthy English versions. Regardless of which form they first produce, ask them to try converting their idea into the other form in order to give them practice working with both symbolic and English expressions.
The need for students to create their own definitions usually arises within the first few days of work. In one class, a student claimed, "If you have an odd number of dots with a jump size of 2, you will make a star." Her comment led to a wonderful discussion about what each student meant by "star." The confusion forced the students to write formal definitions of the shapes that they wanted the word "star" to include. Some wanted any figure with segments that cross to be a star. Another student, because of the conjecture she was working on, defined a star to be a figure such that the two segments coming from each vertex connected to dots that were adjacent to each other. This dialogue led to a discussion about how to write clear definitions (see Definitions) and about the value of agreeing on a common definition.
As students develop conjectures, they should focus their energies on looking for counter-examples to their claims. Students may be too willing to trust their first impressions and to seek only confirming examples. They need to consider what the characteristics of a counter-example might be and then actively look for one. They should not see the discovery of a counter-example as a failure, however. Rather, it is both a sign of their thoughtfulness and the possible start of a new and better theory (see Testing Conjectures for more on the possible fates of conjectures).
Particularly with younger kids, there is a wide gulf between the ideas with which they grapple verbally and their ability to write a clear statement of those ideas. They need to learn the mathematical vocabulary and formal structures that make writing a logical claim easier. Remind them at the start that they should only use words that have a precise meaning. For example, it may seem satisfactory to say that a "star" has sides that "cross." A classmate, however, may argue that two sides are crossing when they intersect at their endpoints. A cycle of peer evaluation and rewriting can be a productive path to better conjectures. Classmates are usually quite good at finding alternative interpretations of confusing statements. Peer review also helps the class develop a sense of itself as a mathematical community.
Once an individual or group has a clear and well-tested conjecture, they should seek to develop an explanation for why their conjecture is true. They should try to appeal to known properties from geometry, arithmetic, and number theory to justify the patterns they have discovered. Just recognizing that factors and primes are involved is an important first step. However, students may not be able to conclude their efforts with a satisfactory proof of their conjectures. Younger students may not even have sufficient background to prove any but the simplest of their claims. Nevertheless, they should still be given positive feedback for the creativity, persistence, and effectiveness they exhibit during each stage of the research process (see assessment).
SAMPLE STUDENT WORK
Thanks to Drew Curtis and his fifth graders at The Neighborhood School, Jamaica Plain, Mass., for their contributions.
The student work discussed here comes from reports written by six fifth-grade students. This group asked dozens of questions, including the following:
- Which combinations of dot number and jump size make stars?
- What combinations of dot number and jump size lead to squares?
- For which dot numbers will every jump size hit every dot?
- How many regions do the segments and the circle create? (For example, a circle with 5 dots and a jump size of 1 produces 6 regions. The same circle with a jump size of 2 yields 11 regions.)
- What happens if we randomly pick a number between 1 and the number of dots each time we jump?
What follows are samples from some student reports, which give a sense of how different students explored the same setting. Parenthetical comments highlight certain issues raised by these students’ statements. As a class activity, you can hand out a sheet of student comments and ask the class to distinguish observations from conjectures (sometimes the dividing line is not clear) and to test the accuracy of each statement. Then ask them to rewrite any conjectures they believe need to be written more clearly.
Alea’s Observations
On a 10-dot circle, 9 and 1 are equal and 2 and 8 are equal. When I say they are equal, I mean those number jump sizes make the same shape. (Note that Alea realized that she had to write a definition for "equal." In this case, "equal" referred to the final shape and not to the actual jumps that made the shapes.)
If you have 11 dots, all of the jump sizes will hit all of the dots.
If you have 13 dots, all of the jump sizes will hit all of the dots.
If you make a star with a jump size of 2, you will hit all of the dots. (Although Alea listed this as an observation, it is really a conjecture about the infinite class of circles with odd dot sizes.)
Alea’s Conjectures
If you have an odd number of dots with a jump size of 2, you will make a star.
Starting at a circle with 5 dots, all the jump sizes will hit all of the dots. Then increase the number of dots by 2 and then by 4 and if you keep increasing by 2 then 4 then for each of these dot numbers all jump sizes will hit all of the dots. (Alea’s pattern generates the sequence 5,7,11,13,17,19,…, which runs out of primes at 25.)
If you have an odd number of dots and an odd jump size, you will get a star. (Again, another conjecture that works for many examples but has counter-examples as well.)
Bryant’s Conjectures
With a jump size of 2 and different dot sizes the pattern goes: half the dots, all the dots, etc.
Any dot size with 1 as the jump size will hit all of the dots. (These conjectures suggest a study of the portion of dots hit for different jump sizes and the periodicity of that portion.)
To get a square, you put any number times 4 for the dot size. Then you take the number you started with as the jump size.
Julia’s Observations
If you have a circle, if you look at a dot, the number [horizontally] across from it in the circle added to the first dot number will equal the number of dots in the circle.
Julia’s Conjectures
For a jump size of 1, you will get one more region than the dot number.
If you add the number of dots to the jump size, this jump size will make the same shape as the original jump size. (Julia is noting the modular nature of the problem.)
Sarah’s Observations
For all prime numbers less than 20, all of the jump sizes except for 1 make stars.
54 of the 100 circle patterns we did were stars. (This observation raises the question about the ratio of patterns overall that are stars.)
From dot numbers 1 through 20 and a jump size of 3, 1/3 of the dots are hit for all multiples of 3.
Sarah’s Conjectures
You will get the same shape for two different jump sizes if the jump sizes added together equal the number of dots in the circle. (This conjecture is the generalization of Alea’s first observation.)
If the number of dots is 3 times the jump size, you will get a triangle. (Here Sarah has identified a sufficient condition for the production of triangles.)
To get a pentagon, the number of dots has to be 5 or a multiple of 5. (This claim involves a necessary but not sufficient condition for a pentagon. It is unlikely that Sarah was thinking about the last two problems differently, since she was able to readily generate dot number and jump size examples for both triangles and pentagons. However, her second claim is a weaker one in that a dot number that is a multiple of 5 need not produce a pentagon.)
Work from Other Classes
Middle school students created the following conjectures:
- The bigger the jump size, the smaller the shape inside the star, and the smaller the angles of the star.
- The shape will be the same if you multiply the jump size and dot number by the same number (i.e., S(d, j) = S(kd, k j)).
- This wonderful quote comes from a student’s note to her mentor:
I noticed something which may be completely irrelevant to anything, but I thought I'd better say something about it just in case: take the 12-pointed circle, for example. The 12-sided polygon is made using jumps of 1 or 11, divide 11 by 1 and you get 11, which is 1 less than 12. A 6-sided polygon is made by jumps of 10 and 2, divide 10 by 2 and you get 5, which is 1 less than 6. This rule was the same for all of the other polygons formed, therefore: the number of sides of the polygon is equal to the largest number of jumps used to form it divided by the smallest number of jumps used to form it + 1. Is that of any use???!
QUESTIONS FOR CONNECT THE DOTS
Research settings do not have guiding questions, so a research agenda will only materialize once students begin to pose their own questions about the setting. Some of their questions will be about the setting and some will be about changes to the setting. For example, one variation, posed by Juancho, was, "What if each jump is a random [whole] number less than the number of dots?" When the students played with the program that this question inspired, they realized that they needed a new set of mathematical questions and ideas. The importance of primes and divisibility faded away. Instead, Juancho’s classmates posed questions such as, "How many jumps on average will it take until you return to the beginning?" This question makes us look at expected value and other probability concepts. Another version of the original problem came from Julia, who asked what shapes would emerge if we jump first by 1, then 2, then 3, etc. This change makes us look at
sequences and series. Both Juancho’s and Julia’s jumping methods raise the question of whether their figures ever had to stop (i.e., return to the 0 dot).
In one middle school class, the students generated dozens of variants on the Connect the Dots setting including the following:
- What if we jump with arcs instead of segments?
- What if there is a dot in the middle of the circle?
- What happens if there are concentric circles with dots?
- What if we use a different shape, such as a sphere or dodecahedron?
These questions involved tweaking some aspect of the original problem, but they were not well defined. What constitutes a jump in these problems? How does the new dot, circle, or shape affect the creation of shapes? Students can discover the gaps in their questions by asking classmates to try to generate examples. Their peers will quickly seek clarification of unexplained aspects of the question. These new problems might lead to interesting investigations once their authors create a complete description of what they are.
Sometimes, a student’s accomplishment is simply the question itself. A class will not have the time to explore all of the questions posed, but we try to emphasize how important it is to ask original and interesting questions. Sometimes students will raise questions that they do not have the background to solve. This gap may motivate them to discover the tools they need. At other times, you may need to help students identify and learn the ideas that will point them in a more productive direction.
Experimenting with the jump size variable can produce surprising results. Sometimes students assume that the jumps have to be whole numbers (the name Connect the Dots reinforces this assumption). A class will usually hit upon the question, "What if the jumps are fractions or negative numbers?" The introduction of rational jump sizes provides an opportunity to test many of the results that the class has already discovered. Do these old claims still hold when we allow rational jump sizes? Would any of the conjectures, such as "You cannot make a rectangle" or "In order to make a square, the dot number has to be divisible by 4," change?
If students begin to exhaust the potential of their own questions or seem ready for a new challenge, the following questions may be of interest:
- Which shapes can we get? If sequences of different sized
jumps are included, can we make a right triangle? A trapezoid
that is not a parallelogram? A parallelogram that is not
a rectangle? Why or why not?
- A student made the picture below with the program Connect
on a TI-73, using 117 for d and 17 for j.
The apparent shape is an annulus (a ring). Is the area of
the annulus really covered? Can you prove that it is or
identify a point in the region that no jump segment hits?
(Note that the discrete nature of computer screen pixels
often leads to misleading images.) What are the answers
to the above questions if the dot size is an integer and
the jump size is
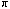 ,
the square root of 3, or any other irrational quantity?
(Try an example using Connect.)
,
the square root of 3, or any other irrational quantity?
(Try an example using Connect.)

A Connect diagram using d = 117 and j = 17
- Students can generate and then study the patterns made by Spirograph®
toys (in which a gear with j teeth rolls within
a ring of d teeth). If you do not have the toy,
a free computer version, Spiral Graphics, is available for
the Macintosh at www.kidsdomain.com/down/mac/spirograph.html
and allmacintosh.xs4all.nl/preview/207667.html;
a Java version for both Windows and Macintosh computers
is available at www.wordsmith.org/~anu/java/spirograph.html.
See "Because a door has to be open or closed: An intriguing problem solved by some inductive exploration" (p 222-28) in Problem posing: Reflections and applications edited by Brown, Stephen and Walters, Marion (1993). Hillsdale, NJ: Lawrence Erlbaum Associates. This essay discusses the connection between Spirograph® designs and a circular version of the locker problem. The circular locker problem begins with a circular room with closed lockers numbered 1 through n; lockers 1 and n are adjacent. As each student enters, Student Number s starts at Locker s and keeps flipping the doors every s lockers (2s, 3s, etc.), wrapping around whenever Student s gets beyond n. A teacher stands at Locker Number n and makes Student s sit down whenever Student s opens or closes the door of Locker n. Describe the travels of each student. What will be the state of the
locker doors after all n students have taken their turn? What are the connections between this locker problem, Spirograph® patterns, and the Connect the Dots patterns?
- A problem that is similar in feel to Connect the Dots but that requires modular arithmetic more explicitly from the beginning is described in an article by Iris Johnson (1998, April), "Paving the way to algebraic thought using residue designs," Mathematics Teacher, pp. 326-332, which presents many student conjectures.
Additional Resources
Students often experiment with sequences of jumps (jump by 3, then 1, then 3, then 1, etc.).
The program CONNECT2 allows them to enter such a sequence (in the form {3, 1}) and see what happens:
TI-73
TI-83
TI-92
For a sequence of random jumps, students can try the program JuanchoC:
TI-73
TI-83
SOME RESULTS AND PARTIAL RESULTS FOR CONNECT THE DOTS
- Which combinations of dot number d and jump size j make stars?
Let us start by defining the effective jump size. Jump sizes of j and d – j generate the same shapes, and jump sizes greater than d generate the same shape as j mod d (the remainder when the jump size is divided by the dot number). These two equivalences map all jump sizes to the interval [0, d/2] through the formula EffectiveJumpSize = min(j mod d, (d – j) mod d).
S(d, j) will be a simple closed figure, and also a regular polygon, only when the number of dots is divisible by the effective jump size. In all other cases, a star (that is, a self-intersecting figure) will arise.
- The jumping process ends when a jump terminates on the starting point after some number of complete trips around the circle. Using a table (see above) to organize the number of trips for different values of d and j, we can make a number of observations. For instance, when d is prime, the number of trips equals the jump size. The same is true when d and j are relatively prime. However, when d and j have a common factor, the number of trips decreases proportionally. These observations combine to yield the following theorem:
Theorem: The
number of trips, t, that a shape completes around
the circle is 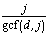 .
.
Proof: The total number of steps jumped is t times the dot number, d. The total distance is also some multiple, n, of the jump size, j. These two facts yield the equation dt = nj. There are an infinite number of pairs of n and t that solve this equation. We want the smallest n that accomplishes the task in order to generate the smallest t. Larger values of n and t that satisfy the equation represent a shape that has reached the starting point, moved past it, and is repeating jumps. Since d and j are fixed and n and t are not, let us separate the variables in dt = nj accordingly:
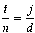
One solution to the equation would be to have t = j and n = d. We can find the smallest possible values for n and t when the fractions are in lowest terms:
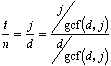
So, 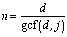 and
and 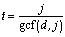 are the smallest solution pair. Q.E.D.
are the smallest solution pair. Q.E.D.
Although the proof above only considers integer values for the jump size and dot number, the result works for real values as well. To state this new conjecture, let us first extend the idea of a greatest common factor to real numbers and introduce the following definitions:
Pseudo-factor: A number, f, is a pseudo-factor of a number, n, if there exists an integer, I, such that fI = n (that is, f divides into n evenly).
mcp (maximum common pseudo-factor): The mcp(a, b) is the largest real number that is a pseudo-factor of both a and b. If a and b lack a common pseudo-factor, then the mcp is undefined.
We can restate the above formula for the number of trips
for real j and d as 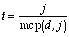 .
For example, when the jump size is 1.5 for a circle with
five dots, there will be
.
For example, when the jump size is 1.5 for a circle with
five dots, there will be 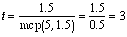 trips. What happens when the two inputs are incommensurable
(e.g., j =
trips. What happens when the two inputs are incommensurable
(e.g., j = 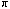 and d = 7)? By definition, there is no number,
no matter how small, that divides evenly into two incommensurable
quantities. In this case, the mcp is undefined. The number
of trips is also undefined because the figure will never
return to the starting point. There is no multiple of
and d = 7)? By definition, there is no number,
no matter how small, that divides evenly into two incommensurable
quantities. In this case, the mcp is undefined. The number
of trips is also undefined because the figure will never
return to the starting point. There is no multiple of
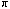 that equals a multiple of 7 (if there was, for example,
m
that equals a multiple of 7 (if there was, for example,
m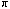 = n7, then we could write
= n7, then we could write 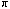 as a ratio of integers, but
as a ratio of integers, but 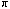 is irrational).
is irrational).
- For which d will every j, j < d, produce a shape that hits every dot? (We are only considering whole numbers j and d.)
Lemma: The first dot to be hit twice will be the starting dot.
Proof: We will use a proof
by contradiction. Assume that two jumps, jump numbers
j1 and j2 both
less than the jump that returns to the starting point,
hit the same non-starting dot; it then takes j2 – j1
jumps to go around the circle an whole number of times.
So, jump number j2 – j1
must have returned to the starting dot. But j2
– j1 < j2
which contradicts our claim that a different dot was hit
for the second time on jump number j2
before any other. Therefore, the starting dot must be
hit first.
Theorem: The shape hits every dot for every j < d only if the dot number is prime.
Proof: This claim is a corollary to the theorem above. If
the jump size and dot number are relatively prime (gcf(j,
d) = 1), then, by the trip
theorem above, t = j. Since the
number of jumps is the total distance divided by the jump
size, there will be 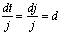 jumps. The d jumps will land on the d
different dots (by the lemma above).
jumps. The d jumps will land on the d
different dots (by the lemma above).
Only when d is prime will all j < d be relatively prime to it. Q.E.D.
Note that when a jump size and dot number have a common factor, the figure does not hit all of the dots. If gcf(j, d) > 1,
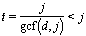 .
.
Since t < j, 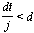 ,
which tells us that the number of jumps is less than the
number of dots.
,
which tells us that the number of jumps is less than the
number of dots.
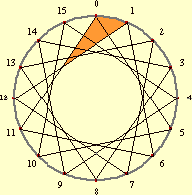
- How many regions do the segments and the circle form?
A hint: Consider a combination of jd + 1 and the gcf(j, d) and study the diagram below. There are also some special cases you need to identify.
- Does a figure of infinite jumps made when the dot number and jump size are incommensurable cover all of the points in the annulus? No.
Theorem: There are points within the annulus that are not covered by such figures.
Proof: Consider a radius of the circle and the segment AB that is the portion of the radius lying within the annulus:
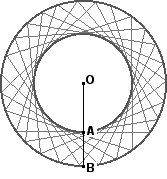
The segment contains an uncountable number of points (see Infinity). By the nature of the Connect the Dots process, the number of segments in the figure is countable (i.e., we can count them as they are drawn one after another). Since each of these countable segments can cross segment AB at most once, there are at most a countable number of covered points in segment AB. When a countable subset is removed from an uncountable one, the remaining set is uncountable. This argument applies to all radii in the circle; therefore, most points within the annulus are not covered by the figure. Q.E.D.
Note that the only reason drawings lead us to think that the ring is covered is because we draw segments with a thickness they do not actually have.