
It's not too difficult to construct a triangle with side lengths that are all positive integers—i. e., whole numbers. All you need to do is pick three numbers (a "triple") such that the sum of any two is greater than the third, such as (12, 19, 21). Then imagine taking three sticks with these lengths and connecting their ends. The triangle you get with (12, 19, 21) will be acute:
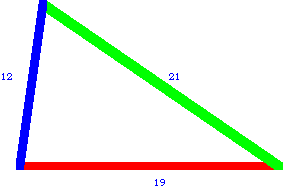
How about right triangles? Can you find triples of positive integers (a, b, c) so that the triangle with these side lengths is a right triangle?
You may have already seen examples of right triangles with integer side lengths. Two simple ones are (3, 4, 5) and (5, 12, 13):
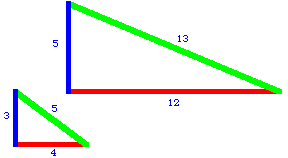
Can you come up with more? What questions can you pose about the numbers in these triples? What questions can you ask about the set of all Pythagorean triples?