Teaching Notes for Pythagorean Triples

We assume that your class is familiar with Pythagoras' Theorem and how it characterizes right triangles.   Although the study of Pythagorean triples can be conducted purely with numbers, the geometric connection is likely to make the problem less abstract to your students.   

Phase 1:  Establish the setting

Start by displaying the equation 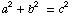and see how your students react.   Ask them what they think of when they see this equation.  Here are a few possible reactions:

1.   You  get some solutions for a, b, and c, such as  
    (a)   3, 4, 5
    (b)  1, 1,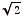
    (c)   0, 1, 1
    (d)  -5, 12, -13
    (e)  1, 1, 2
    (f)  15, 20, 25
    (g)  0, 0, 0

2.  Someone volunteers the response "Pythagoras' Theorem" or "right triangle."  

Try to get both types of responses, including several solutions.  Discuss the distinction between the solutions that represent side lengths of a right triangle and those that do not.   

Be prepared to respond to non-solutions like 1, 1, 2.  Explain that you want to begin an investigation of right triangles with integer sides, so responses like (b), (c), (d), and (g) will be ruled out.   If solutions like this don't come up, you might want to contribute them to the list for completeness. Although responses like (f) may not be considered of interest later, don't be so restrictive at this point.

Explain that the class will be looking for Pythagorean triples 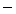solutions in the positive integers.  Propose that you will start by looking for as many Pythagorean triples as possible.  You might want to reinforce the idea using the Problem Statement and note that plenty of triangles have three integer sides, but many are not right triangles.  Give the class some time to come up with more examples.  If you think it would be useful, you could distribute the list of squares below.

List of Squares, 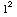through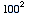

Pythagoras' Theorem - a proof with no words

You might want to review Pythagoras' Theorem.  There are many nice "proofs without words" that might give your students a new perspective on the theorem.   The following proof, which comes from a Chinese source, is over 3000 years old, written long before Pythagoras was born.

Consider the arrangement of four copies of the same right triangle as below,  with a blue-green square in the middle.

Rearrange the triangles in pairs as you see below.  Notice that there is room for two smaller blue-green squares.   Let your students ponder what these two figures imply!

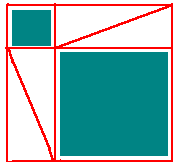
Close this phase by asking that each person in the class find at least 10 Pythagorean triples before you begin the next phase.

Phase 2: Look for patterns

Make a list of the Pythagorean triples your class has come up with.  Ask the students how the list might be organized.  For example, you might want to sort the individual numbers of each triple in ascending order;  and then sort the triples according to the first number.   Alternative approaches should be tried, because different ways of organizing the data may lead to different types of conjectures. Collect examples until you have some variety,  not all just multiples of one triple, like  3-4-5, 6-8-10, 9-12-15, . . . .      Stop and ask for observations.   See if your students identify patterns or ask questions.  If students don't bring it up, raise the issue of whether there are an infinite number of Pythagorean triples.  At some point you'll want to define a primitive Pythagorean triple, i. e., a triple with no common factor greater than 1.   This will rule out  6-8-10, 9-12-15, 12-16-20, 10-24-26, ...   which should make the question more challenging.  

Put together a new list of primitive Pythagorean triples.  It will be more difficult for your students to come up with many of them; so if they don't offer at least eight examples, you might want to add some of these:

Give the class time to look for patterns among the triples they have to work with.   Use a few of the triples in the list above to check any conjecture they might have.  Close this phase by asking the class to continue looking for patterns and to think about how to find more triples.

Phase 3:  Develop Some Theory

In this phase, the ultimate goal will be to establish that there are an infinite number of primitive Pythagorean triples.  Even if your class doesn't develop a formula that generates all triples, just proving their infinitude using one category of triples should be considered a significant result.

Summarize the observations that the students have made so far.  Here are a few questions that they may have raised by now:

• How many even numbers can there be in a primitive Pythagorean triple?
• Can an even number be the largest number in a Pythagorean triple?
• Can an even number that appears in a Pythagorean triple be two times an odd number?
• Are there an infinite number of triples with the smallest element odd and the other two elements one apart?

Answering these questions will lead students to some important observations that will help them develop a formula for all Pythagorean triples.   One observation is that one of the legs needs to be even and the other odd.  There are two other key questions that follow from this observation.   

Consider the case when  a is even. We also have .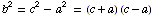
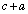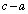1.   Could   and   have a common factor greater than one?
2.  What does your answer say about 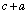   and ?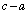

There are several steps involved in getting to this last question, and several more to work through until you reach this conclusion: Every primitive Pythagorean triple takes the form 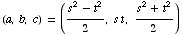 , where s and t are relatively prime odd integers,  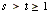.  Don't be concerned if your class doesn't get this far.   You might be inclined to fill in a few more details at this point, but  give them a chance to struggle with the ideas first. Proving some of the initial conjectures about the parity of the lengths or about special triples such as { 2a+1, 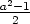, 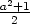} or { 4a, 4a²-1, 4a²+1 } are considerable accomplishments.

If they get bogged down, you might want to take a detour to a different direction that provides an infinite, yet simpler, family of Pythagorean triples.  It's not too difficult to prove that the sum of the first n odd positive integers is 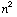.  Here's a proof with no words:

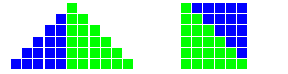
Fibonacci, in The Book of Squares,  uses this fact to derive his first result on Pythagorean triples.   Hint:  Consider the sum of the odd positive integers up to 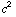, where c is any odd positive integer greater than 1.   What distinguishes this family of Pythagorean triples?  Emphasize to your class that they now have a way to get an infinite number of Pythagorean triples.  Once you've reflected on the significance of this result, you can go in one of the following directions.
    1.  You can resume working on the general problem of finding all Pythagorean triples.
    2.  Since Fibonacci's first family of triples has the property that the hypotenuse and a side differ by one, is there a similar family where the difference between hypotenuse and longer side is two?  three?   k?
    
Did you finish what is suggested here? Where do you go next?  See the Resources page for some ideas.

---