Warm Up Problems for Marion Walter's Theorem
1 Consider 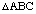 with its three sides trisected and lines drawn as indicated in Figure 3.
with its three sides trisected and lines drawn as indicated in Figure 3.
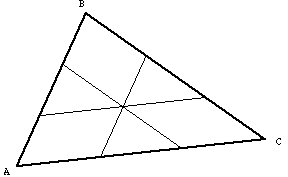
Figure 3
(a) What is the length of 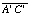 in terms of
in terms of 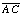 ?
?
(b) Will these three lines always meet at one point as they appear to meet in the figure?
2. Suppose that the sides of 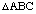 in Figure 4 are divided into 5 equal parts and the division points that are closest to the vertices are connected as indicated in the figure below, with inner triangle
in Figure 4 are divided into 5 equal parts and the division points that are closest to the vertices are connected as indicated in the figure below, with inner triangle 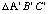 formed from their intersection.
formed from their intersection.
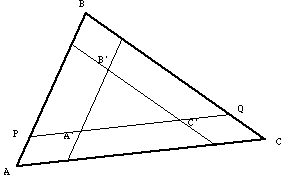
Figure 4
(a) What is the length 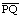
 in terms of the length of
in terms of the length of 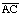 ?
?
(b) What is the length of 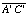
 in terms of the length of
in terms of the length of 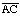 ?
?
(c) What is the area of 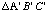 in terms of the area of
in terms of the area of 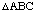 ?
?
(d) What are the areas of the diamond shaped regions at corners of these figures in terms of the area of 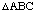 ?
?
(e) Find some other relationships in the figure.
3. The equilateral triangle with thick lines in Figure 5 has area 1 and is rotated about its center 40 degrees and 80 degree to form the other two triangles. What is the area of the inner nonagon?
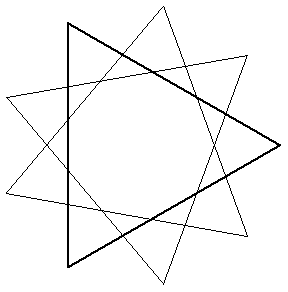
Figure 5
4. (a) Given four positive numbers a, b, c, and d, consider the points O(0,0), Q(a,c), R(b,d), and 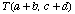 . Find the area of parallelogram OQTR depicted in Figure 6.
. Find the area of parallelogram OQTR depicted in Figure 6.
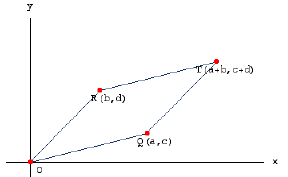
Figure 6
(b) You are given points A(0,0), B(1,0), and C(0,1), and numbers a, b, c, and d such that 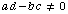 . Suppose that A'B'C' is the triangle obtained by transforming each point on the original triangle by the rule
. Suppose that A'B'C' is the triangle obtained by transforming each point on the original triangle by the rule 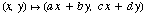 . How are the areas of triangle ABC and A'B'C' related in terms of a, b, c, and d? Inititally you can think of the values of a, b, c, and d as positive, but your answer should be correct for all possible values.
. How are the areas of triangle ABC and A'B'C' related in terms of a, b, c, and d? Inititally you can think of the values of a, b, c, and d as positive, but your answer should be correct for all possible values.
5. Consider triangle ABC with the following trisection points,
(1) P on segment AB closest to B
(2) R on segment BC closest to C and
(3) Q on segment CA closest to A,
as in Figure 7. If these points are connected by segments to the opposite vertices of the triangle, is the area of the inner triangle created by the segments related to the area of triangle ABC?
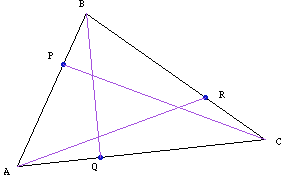
Figure 7

We do not include results for this warm up problem on the Making Mathematics web site.