Hints for Marion Walter's Theorem
Figure 1, the figure that was in the project statement section, was drawn using Geometer's Sketchpad and the areas are only approximate numbers.
Dynamic geometry software is an indispensable tool for this project. Basically, you should make each construction, deform it, and look for invariants. For example, if you could show that the ratio of the area of the hexagon to the area of the triangle is invariant under dragging, all you would need to do is prove the result for, say, an equilateral triangle. Does that make it easier?
If you decide to use classical geometry...
Think about the ways that you can cut up the triangle you start with using the various lines in the problem.
If you decide to use analytic geometry or vector geometry...
You can assume that one of the vertices is the origin, and one of the other vertices is on the positive x-axis. A mathematician would say "Without loss of generality, let A be at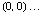 
. This "mathspeak" for "if it's not true, we can make it true." For example, if A isn't on the origin, we'll just move the origin. That doesn't change what we're going to prove anyway.
