Teaching Notes for Marion Walter's Theorem

Day 1

If you have access to dynamic geometry software you can start by showing your students a dynamic version of Figure 1 in the project statement.

Ask your students if they think it's possible for the inner polygon to have anything other than six sides.   

Ask them to draw the corresponding figure for special triangles (equilateral, isosceles right, 30-60-90, ...) to see what the relationship is in these cases.  

Day 2

See if anyone has new conjectures or ideas.  Discuss what it will take to prove them.

Have your students do a few of the warm-up problems.  Be open to the possibility that your discussion might suggest even better warm up problems than are listed here.

Day 3

There are at least two very different proofs of the conjecture that your students have probably come up with.  If no ideas have emerged, the following discussion points might get them thinking in one of these directions.

Toward proof #1

Ask whether the results for special cases can be used to prove the more general case.  Sometimes you can transform one kind of triangle into another and certain things are invariant.  

Toward proof #2

Discuss how the various areas in the general figure might be added and subtracted to produce the area of the inner hexagon.   Use this much simpler example to illustrate the basic strategy.
If a equilateral triangle with unit  area  is rotated 60 degrees to form Figure 8, the triangles that make up the points of the star each have area 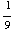  and so the area so the inner hexagon must have area .

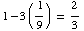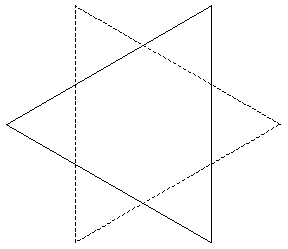
Figure 8

Day 4

Give students an opportunity to report on any progress or ideas they have come up with.

Have them identify characteristics of the problem that they can change to pose new questions.  

---