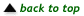Results for the Patterns in Pascal’s Triangle Problem
Solutions to the Warm-up Problems
- See Pascal’s Triangle
at http://www2.edc.org/makingmath/mathtools/pascal/pascal.asp for a
range of possible discoveries.
- Each step removes 1/9 and leaves 8/9
of the remaining black area. After n steps, the original
square will be (8/9)n
black. As this process is continued for ever larger n,
the square will get ever closer to being 0% black. Surprisingly,
this does not mean that the whole figure will be black. There
will still remain a set of black points (of measure zero). Where
are they? Think of the points that are removed at each step
(the interior of each square and not its boundary).
- See the modular arithmetic
resources for the solutions to their problems.
- See the results section
of the trains project.
- Answers for a) , b), and c) are the same as rows 0 through
4 of Pascal’s triangle.
d) f(n, k) = f(n
– 1, k – 1) + f(n –
1, k)
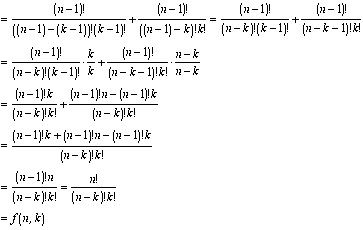
Since 0! = 1, f(n, n) = 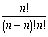 and
f(n, 0) =
and
f(n, 0) = 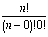 both simplify to 1. Thus, f(n, k)
satisfies the same properties as Pascal(n,
k).
both simplify to 1. Thus, f(n, k)
satisfies the same properties as Pascal(n,
k).
e) For 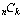 ,
we are choosing a subset of size k from our set of
size n. Arbitrarily pick one element of the set, e.
Each of our k-element subsets either contains e
or does not. So,
,
we are choosing a subset of size k from our set of
size n. Arbitrarily pick one element of the set, e.
Each of our k-element subsets either contains e
or does not. So,
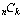 = the number of subsets containing e +
= the number of subsets containing e +
the number of subsets that do not contain
e
If a subset contains e, we still have to pick k
– 1 elements from the remaining n – 1 elements
of the set (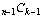 ). If a subset does not contain e,
we have to pick k elements from the remaining n
– 1 elements (
). If a subset does not contain e,
we have to pick k elements from the remaining n
– 1 elements (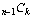 ).
Therefore,
).
Therefore, 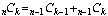 .
.
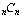 asks for all subsets containing all elements of a set and there
is only one way to do that (take the whole set). Likewise,
asks for all subsets containing all elements of a set and there
is only one way to do that (take the whole set). Likewise, 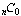 asks for all subsets containing no elements
of a set and there is only one way to do that (use the empty
set). So
asks for all subsets containing no elements
of a set and there is only one way to do that (use the empty
set). So 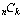 satisfies the same properties as Pascal(n,
k) and f(n, k).
satisfies the same properties as Pascal(n,
k) and f(n, k).
This last proof demonstrates that the arithmetic (add the two
numbers above) and combinatorial (the elements come from 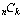 ) ways of defining Pascal’s
triangle are consistent. These two proofs show that the value
of the kth number in the nth row of Pascal’s
triangle (with our counts starting at the 0th value in row 0)
matches the values from the factorial and combinations formulas.
) ways of defining Pascal’s
triangle are consistent. These two proofs show that the value
of the kth number in the nth row of Pascal’s
triangle (with our counts starting at the 0th value in row 0)
matches the values from the factorial and combinations formulas.
Main Results
Because of the many different ways of deriving Pascal’s
triangle, there are many ways to prove discoveries about it. The
following results take different approaches to proving related
findings. Each representation provides insights that combine to
give us a rich picture of the patterns in the triangle.
Thinking about Pascal mod 2 geometrically and arithmetically
(some answers to project question #3):
Although the mod 2 Pascal’s triangle is often compared to
Sierpinski’s gasket, it differs in one important respect: Pascal’s
triangle is discrete. Because of this lack of continuity, the self-similar
scalings are imprecise. For example, the central 0 in the red triangle
in the figure below corresponds with the triangle of six 0’s
in the blue triangle and the triangle of twenty-eight 0’s in
the center of the figure. These two scalings do not maintain a consistent
ratio (although the ratio does tend toward 4, consistent with a
scaling factor of 2). Nonetheless, the figure does display a variant
of self-similarity as we look at ever-larger portions. It is self-similarity
based on translation! Each element has the same parity as that of
the element  rows earlier (for the largest
rows earlier (for the largest
 possible).
possible).
Pascal’s Triangle mod 2 with highlighted
matching regions
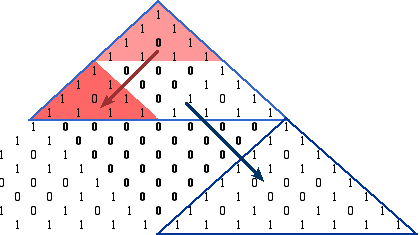
Theorem: For the mod 2 Pascal’s triangle,
each new block of  rows from row
rows from row  through row
through row 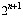 –1
has exactly two copies of the first
–1
has exactly two copies of the first  rows (rows 0 through
rows (rows 0 through  –1) with a triangle of 0’s in between.
–1) with a triangle of 0’s in between.
Proof: We will prove the claim inductively.
We will add the additional claim that row  –1 is composed entirely of 1’s
(odds). We have the base case in row 1, which is two copies of
row 0. The row numbers 0 and 1 are both of the form
–1 is composed entirely of 1’s
(odds). We have the base case in row 1, which is two copies of
row 0. The row numbers 0 and 1 are both of the form –1 and both rows contain only 1’s.
–1 and both rows contain only 1’s.
Let’s now show that if our claims are true for n,
they must also be true for n + 1. If true for n,
then row  – 1 is composed entirely of 1’s. That means that row
– 1 is composed entirely of 1’s. That means that row
 will have 1’s on the ends and
will have 1’s on the ends and  – 1 0’s in between.
This stretch of 0’s will shrink by one 0 per row until they
are gone in row
– 1 0’s in between.
This stretch of 0’s will shrink by one 0 per row until they
are gone in row  +
+  – 1 =
– 1 = 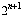 – 1. The two
terminal 1’s in row
– 1. The two
terminal 1’s in row  – 1 will each start the pattern that the 1 in row 0 starts.
These two copies, initially separated by
– 1 will each start the pattern that the 1 in row 0 starts.
These two copies, initially separated by  – 1 spaces, will grow until the separating
0’s are gone in row
– 1 spaces, will grow until the separating
0’s are gone in row 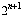 –
1. That is, they will have grown, without interference, for
–
1. That is, they will have grown, without interference, for  rows and each reproduced
the original
rows and each reproduced
the original  rows. Since row
rows. Since row  – 1 had
– 1 had  1’s, row
1’s, row 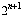 – 1 will have
– 1 will have
 +
+  =
= 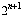 1’s. Thus we have shown that both claims, the
duplication of the prior set of rows and the presence of all 1’s
necessary to establish the conditions for a new round of duplicating,
are satisfied. Q.E.D.
1’s. Thus we have shown that both claims, the
duplication of the prior set of rows and the presence of all 1’s
necessary to establish the conditions for a new round of duplicating,
are satisfied. Q.E.D.
Describing the pattern of odds (a first answer to the
number of odds in row 100):
Although the above ideas may follow an exploration of project
question # 1, it is easier to prove observations about the patterns
of odds following work on question #3.
The geometric duplication process suggests a related method for
counting the number of odds in each row. If S is the
sequence of the number of odds in the rows of Pascal’s triangle,
we can get S from the following procedure: S0
= 1, Sn = Sn – 1
& (2. Sn – 1). Which means:
to get the next sequence, take the last sequence and follow it
(“&” means catenate) with all of the last sequence’s
elements doubled:
S0 = {1}
S1 = {1} & 2.{1}
= {1, 2}
S2 = {1, 2} & 2.{1,
2} = {1, 2, 2, 4}
S3 = {1, 2, 2, 4} &
2.{1, 2, 2, 4} = {1, 2, 2, 4, 2, 4, 4, 8}
This doubling and appending corresponds to the translating and
copying of the geometric description above. If we keep generating
Sn, we find that getting row 100 is not so
labor intensive. Sn has  elements, so the 101st element in S
is in S7. The following commands entered into
a Texas Instruments TI-83 calculator take care of the labor:
elements, so the 101st element in S
is in S7. The following commands entered into
a Texas Instruments TI-83 calculator take care of the labor:
|
Start with S0:
|
{1}  L1
L1
|
L1 is a list variable.
|
|
Build S1:
|
augment(L1, 2*L1)
 L1
L1
|
Augment catenates two lists.
|
|
Build S1 through S7.
|
Press ENTER six times.
|
ENTER repeats the recursive rule.
|
|
To get row 100:
|
L1(101)
|
This is the 101st element in L1.
|
And the 101st element is 8, so there are 8 odds in row 100.
This recursive approach is pretty quick, but what if our calculator
batteries are dead? Is there a more direct way to find the value
in terms of the row number itself?
Explicitly predicting the pattern for any line:
When a problem involves patterns of doubling or trebling, thinking
in terms of base 2 or base 3 representations can lead to insights.
The table below, produced by a Making Mathematics teacher compares
the number of ones in a row’s base 2 representation with
the number of odds in that row.
|
n
|
n in base 2
|
# of 1’s (in base 2)
|
Number of odds in row n
|
|
0
|
0
|
0
|
20 = 1
|
|
1
|
1
|
1
|
21 = 2
|
|
2
|
10
|
1
|
21 = 2
|
|
3
|
11
|
2
|
22 = 4
|
|
4
|
100
|
1
|
21 = 2
|
|
5
|
101
|
2
|
22 = 4
|
|
6
|
110
|
2
|
22 = 4
|
|
7
|
111
|
3
|
23 = 8
|
|
8
|
1000
|
1
|
21 = 2
|
Why does this pattern seem to work? One explanation comes from
the self-similarity rule and the doubling procedure for S.
These imply the following:
Let f(n) be the number of odd
entries in line n of Pascal’s triangle, then 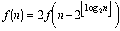 .
.
This function is equivalent to moving up the triangle by the
highest power of 2 possible (to the line that we duplicated to
make line n). For example f(27) = 2 f(27
– 16) = 2 f(11). But what is f(11)? Well,
reapplying the formula yields f(11) = 2 f(11
– 8) = 2 f(3). Continuing, we get f(3)
= 2 f(3 – 2) = 2 f(1) and f(1)
= 2 f(1 – 1) = 2 f(0) and f(0)
= 1. Putting that recursive sequence altogether gives f(27)
= 24. Each of the factors of two was contributed when
we subtracted the highest power of two possible and these are
each represented by a 1 in the base 2 representation of 27 (2710
= 110112). In general, iterative application of the
above formula will lead to f(0) after as many recursions
as the number of 1’s in n’s base two representation.
This rule corresponds nicely with the 1, 2, 2, 4 pattern because
the rightmost digits of the counting numbers in base 2 cycle through
00, 01, 10, and 11 (and lead us to think about the fractal nature
of counting in any base).
An algebraic finding:
Here is an excerpt from one Pascal explorer’s report:
“I have been using the factorial formula to prove that the
scaling patterns in Pascal always work. I was able to show that
the parity of 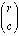 matches that of
matches that of 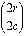 .
However, that scaling leaves lots of gaps. If we know the first
four rows or Pascal, doubling all of the coordinates just gives
us the parity of the even entries in rows 6 and 8 (for example,
.
However, that scaling leaves lots of gaps. If we know the first
four rows or Pascal, doubling all of the coordinates just gives
us the parity of the even entries in rows 6 and 8 (for example,
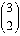 is odd,
so
is odd,
so 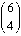 must
be, too). I then moved on to proving the parity of the elements
that neighbor those that have even row and column numbers when
I discovered what I think is a strange little observation. I was
trying to prove: If
must
be, too). I then moved on to proving the parity of the elements
that neighbor those that have even row and column numbers when
I discovered what I think is a strange little observation. I was
trying to prove: If 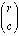 = 0 then
= 0 then
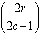 = 0. Here is what I found:
= 0. Here is what I found:
Meg’s Little Observation Theorem: Odd and even numbers can
appear in Pascal’s triangle for three of the four cases of
odd and even row and column numbers. However, when the row is
even and the column is odd, the entry is always even.
Proof:
Case 1: row is odd, column is odd. Proof by example: 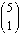 = 5 and
= 5 and
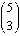 = 10
(so we can get an odd or even result).
= 10
(so we can get an odd or even result).
Case 2: row is odd, column is even. Proof by example: 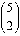 = 10
and
= 10
and 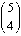 = 5.
= 5.
Case 3: row is even, column is even. Proof by example: 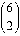 = 15
and
= 15
and 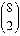 = 28.
= 28.
Case 4: row is even, column is odd. The even row is 2r and the
odd column is 2c-1.
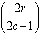 =
=
We know that this entire expression is an integer. Since the denominator
of the final factor consists of all odd terms, the initial factor
of 2 remains and the result is even. Q.E.D.
My question is why?! What is special about these combinations that
they must be even? Interestingly, the pattern of alternating zeroes
in every other line had not caught my eye because of the stronger
triangular patterns (see the picture below).”

The above result is summarized in the table below.
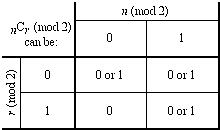
Possible remainders for different 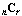 mod 2
mod 2
Variations also arise with 3 as the modulus (see below). These
two tables hint at a number of possible generalizations. Are these
generalizations valid? Are they limited to moduli that are prime?
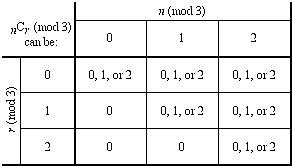
Possible remainders for different 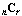 mod 3
mod 3
Thinking about Pascal mod p arithmetically (some
answers to project question #4):
There are eight odd numbers in the 100th row of Pascal’s triangle, 89 numbers that are divisible by 3, and 96 numbers that are divisible by 5.
Of course, one way to get these answers is to write out the 100th
row, of Pascal’s triangle, divide by 2, 3, or 5, and count (this
is the basic idea behind the geometric approach).
But let’s see if we can find a more efficient (and elegant)
way to get our answers. In an attempt to show how one might actually come up with
interesting results, what follows is a collage of various arithmetic
approaches that we’ve seen over the years in our work with
students and teachers.
We want to count the number of elements in a row of Pascal’s
triangle that are (or are not) divisible by some integer. Divisibility by
a prime is easier to deal with, so let’s look at that case. The question,
then, is
Given a non-negative integer n and a prime p, which numbers 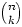 are divisible by p?
are divisible by p?
Well, sometimes a more pointed question is easier to answer:
Given a non-negative integer n and a prime p, what is the highest power of p that divides 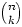 ?
?
This “highest power of p” function is useful in many contexts, and it’s
sometimes denoted by ordp, so, for example:
| ord5(40) |
= 1 (20 = 51 . 23) |
|
|
| ord2(40) |
= 3 |
|
|
| ord7(40) |
= 0 |
|
|
| ord7(58 . 34 . 5 . 72 . 115) |
= 2 |
|
|
To get ordp(n), factor n into primes and look at the power of p that shows up. That’s ordp(n). You can check that ordp has the property that, for non-negative integers m and n,
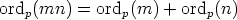 And, if n is a factor of m,
And, if n is a factor of m,
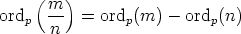
So, our question becomes
Given a non-negative integer n and a prime p, what’s an easy way to calculate ordp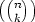 ?
?
In particular, we want to know when
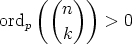 because this is when p is a factor of
because this is when p is a factor of 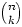 .
Of course, what we really want to do is to count all the entries in the nth row of Pascal that have ordp > 0, but let’s worry about that later.
.
Of course, what we really want to do is to count all the entries in the nth row of Pascal that have ordp > 0, but let’s worry about that later.
Well, there’s an explicit formula for 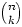 in terms of factorials:
in terms of factorials:
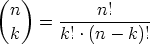 So, using the properties of ord (the ord of a quotient is the difference
of the ords, and the ord of a product is the sum of the ords),
we have
So, using the properties of ord (the ord of a quotient is the difference
of the ords, and the ord of a product is the sum of the ords),
we have
ordp 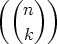 |
= ordp 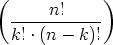 |
|
|
|
= ordp(n!) - ordp(k!) - ordp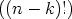 |
|
|
It seems like a next step might be to find a way to find the ord
of a factorial. A numerical example points the way: let’s
calculate ord 3(139!). So, we want to find the highest power of 3 that divides
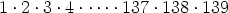 Each multiple of 3 give us at least one “contribution”:
Each multiple of 3 give us at least one “contribution”:
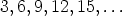 This stops at the last multiple of 3 before 139 (that is, at 138),
and there are about
This stops at the last multiple of 3 before 139 (that is, at 138),
and there are about 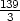 numbers in the list. In fact, there are exactly
numbers in the list. In fact, there are exactly
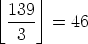 where
where 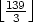 means the “integer part” of 46
means the “integer part” of 46 (that is, the integer part of
(that is, the integer part of 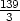 ).
).
Of course, we’ve missed some “extra” multiples
of 3: every multiple of 9 (that is, 9, 18, 27... ) counts twice, and there are
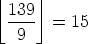 of these. But, we’ve now missed the extra multiples of 3 that
come from multiples of 27, and there are
of these. But, we’ve now missed the extra multiples of 3 that
come from multiples of 27, and there are
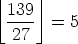 of these. You get the idea. Next, we need to count the multiples of
81 (to get the extra factor that comes from 34), and there are
of these. You get the idea. Next, we need to count the multiples of
81 (to get the extra factor that comes from 34), and there are
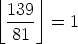 of these (namely, 81 itself). If we didn’t know any better,
we could count the multiples of 243 that are less than 139, and there’d be
of these (namely, 81 itself). If we didn’t know any better,
we could count the multiples of 243 that are less than 139, and there’d be
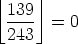 of these. And everything would be 0 from here on. So, the power of
3 that divides 139! is
of these. And everything would be 0 from here on. So, the power of
3 that divides 139! is
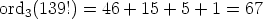 Remember where this came from. Summarizing our calculations, we
could say:
Remember where this came from. Summarizing our calculations, we
could say:
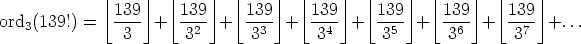 Of course, after awhile (in fact, after 34), all these “floors” are 0. So, we have a method for finding ordp(n!):
Of course, after awhile (in fact, after 34), all these “floors” are 0. So, we have a method for finding ordp(n!):
Proposition 1. If n is a non-negative integer and p is a prime, then
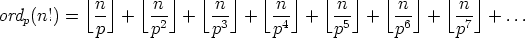
This is unsatisfying in many ways. For one, it doesn’t tell
you when the terms of the sum drop off to zero. For that, you’d have to
write n in base p. But wait—if you write n in base p, the whole sum in the proposition gets easier. Here’s how:
Let’s go back to our example if 139 and 3. First, let’s
write 139 as a base-3 expansion:
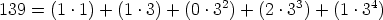 So,
So,
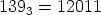
Then, to get ord3(139!), we use the proposition and calculate as follows:
|
|
= 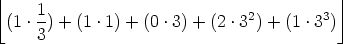
|
|
|
= (1 . 1) + (0 . 3) + (2 . 32) + (1 . 33)
|
|
|
= 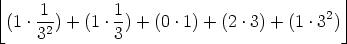
|
|
|
= (0 . 1) + (2 . 3) + (1 . 32)
|
|
|
= 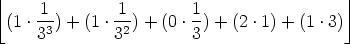
|
|
|
= (2 . 1) + (1 . 3)
|
|
|
= 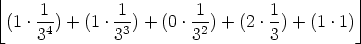
|
|
|
= (1 . 1)
|
And everything is 0 after this. Wow, look at this. Look at the
rightmost equations. One thing we could do is to read down instead of across;
that would allow us to add “like” powers of 3. And, just
like when you read across, when you read down you see the base-3 digits of 139, first
all except the “units” 1, then all except the 11, then
all but the 011, and finally all but the 2011. Will this always happen? Let’s
see. Suppose
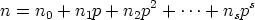
Then

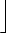
|
= 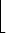 ( n
0 .
( n
0 .
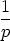 ) + ( n
1 .
1) + ( n
2 .
p )
+ ( n 3
.
p2
) +
) + ( n
1 .
1) + ( n
2 .
p )
+ ( n 3
.
p2
) + 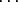 + ( n
s .
p s
- 1
)
+ ( n
s .
p s
- 1
) 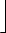
|
|
= (
n
1
.
1) + (
n2
.
p
) + (
n3
.
p2
) +
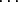 + (
n
s
.
p
s
-
1
)
+ (
n
s
.
p
s
-
1
)
|
and
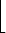
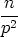
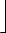
| = 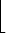 ( n0
.
( n0
.
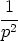 ) + ( n
1 .
) + ( n
1 .
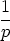 ) + ( n
2 .
1) + ( n3
.
p )
+
) + ( n
2 .
1) + ( n3
.
p )
+ 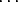 + ( n
s .
p s
- 2
)
+ ( n
s .
p s
- 2
) 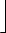
|
|
= (n2 . 1) + (n3 . p) + 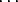 + (ns . ps-2)
+ (ns . ps-2) |
And, more generally,
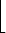 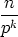 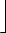 |
= 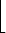 (n0 .
(n0 . 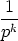 ) + (n1 . ) + (n1 . 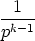 ) + (n2 . ) + (n2 . 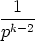 ) + (n3 . ) + (n3 . 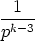 ) + ) + 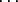 + (ns . ps-k) + (ns . ps-k)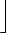 |
|
|
|
= (nk . 1) + (nk+1 . p) + 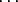 + (ns . ps-k)
+ (ns . ps-k) |
But
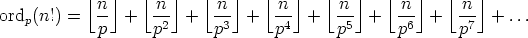
So let’s write this all out and see if we can use the “add
down” trick:
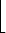  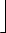
|
= (n1 . 1) + (n2 . p) + (n3 . p2) + (n 4 . p3) + 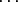 + (n s . ps-1)
+ (n s . ps-1) |
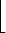 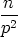 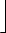
|
= (n2 . 1) + (n3 . p) + (n4 . p2) + (n 5 . p3)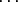 + (n s . ps-2)
+ (n s . ps-2) |
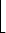 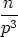 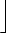
|
= (n3 . 1) + (n4 . p) + (n5 . p2) + 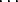 + (n s . ps-3)
+ (n s . ps-3) |
| |


|
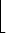 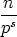 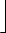 |
= (ns . 1) |
If we add down, we get the “clipped” sum of the base-p digits of n. Let’s invent a notation for this: Let  p(n) be the sum of the base-p digits of n. Then adding down, we have
p(n) be the sum of the base-p digits of n. Then adding down, we have
| ord p(n!) |
= ( p(n) - n0) . 1 + ( p(n) - n0) . 1 + ( p(n) - n0 - n1) . p + ( p(n) - n0 - n1) . p + ( p(n) - n0 - n1 - n2) . p2+ p(n) - n0 - n1 - n2) . p2+ |
|
( p(n) - n0 - n1 - n2 - n3) . p3 + p(n) - n0 - n1 - n2 - n3) . p3 + 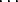 + (
+ ( p(n) - n0 - n1 - n2 -
p(n) - n0 - n1 - n2 - 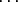 - ns-1) . ps-1+
- ns-1) . ps-1+ |
|
( p(n) - n0 - n1 - n2 - p(n) - n0 - n1 - n2 - 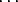 - ns) . ps
- ns) . ps |
The last line is 0, but we put it in to keep the pattern going.
Time for some algebraic fooling around. Gather the  p(n)s, the n0s, the n1s, and so on:
p(n)s, the n0s, the n1s, and so on:
| ordp(n!) |
=  p(n) p(n)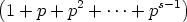 |
|
|
|
- n0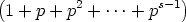 |
|
|
|
- n1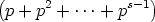 |
|
|
|
- n2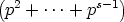 |
|
|
|
 |
|
|
|
- ns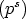 |
|
|
Each sum is a geometric series, just begging to be summed:
| ordp(n!) |
=  p(n) p(n)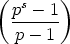 |
|
|
|
- n0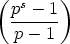 |
|
|
|
- n1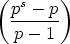 |
|
|
|
- n2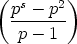 |
|
|
|
 |
|
|
|
- ns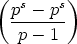 |
|
|
Factor out the denominator of p - 1 and rearrange what’s left:
Oh, how nice: since
n0 + n1 + 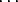 + ns
+ ns |
=  p(n) and p(n) and |
|
|
n0 + n1p + n2p2 + 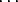 + n sps
+ n sps |
= n |
|
|
this simplifies to
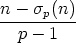 Let’s state it as a result:
Let’s state it as a result:
Proposition 2. If n is a non-negative integer and p is a prime,
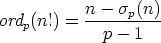 where
where  p(n) is the sum of the digits in the base-p expansion of n.
p(n) is the sum of the digits in the base-p expansion of n.
We can apply this formula to our example and, again, get 67:
We’re in a better position now to evaluate ordp  . In fact,
. In fact,
ordp  |
= ordp 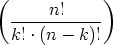 |
|
|
|
|
|
|
|
= ordp(n!) - ordp(k!) - ordp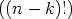 |
|
|
|
|
|
|
|
= n -  p(n) - p(n) - 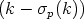 - - 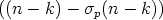 p - 1 p - 1 |
|
|
|
|
|
|
|
=  p(k) + p(k) +  p(n - k) - p(n - k) -  p(n)p - 1 p(n)p - 1 |
|
|
This is pretty interesting. Let’s state it as a result:
Proposition 3. If n is a non-negative integer and p is a prime,
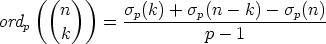 where
where  p(n) is the sum of the digits in the base-p expansion of n.
p(n) is the sum of the digits in the base-p expansion of n.
Notice that what we really care about is which 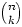 have non-zero ords. But it turns out that one can get the exact value of the expression
in proposition 3 with very little extra work (we know this because we worked it
out before we wrote up these results). The fact that
have non-zero ords. But it turns out that one can get the exact value of the expression
in proposition 3 with very little extra work (we know this because we worked it
out before we wrote up these results). The fact that
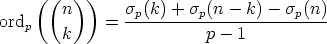 is one of those strange results that contains a surprise: We know
that ordp
is one of those strange results that contains a surprise: We know
that ordp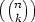 is a non-negative integer, so p - 1 must be a factor of
is a non-negative integer, so p - 1 must be a factor of  p(k) +
p(k) +  p(n - k) -
p(n - k) -  p(n)—that’s not at all obvious. And shouldn’t
the digit sum of n equal the digit sum of k plus the digit sum of n - k? After all, k and n - k add up to n, so shouldn’t the sum of the digits work the same way? Let’s see what happens with
an example:
p(n)—that’s not at all obvious. And shouldn’t
the digit sum of n equal the digit sum of k plus the digit sum of n - k? After all, k and n - k add up to n, so shouldn’t the sum of the digits work the same way? Let’s see what happens with
an example:
Let’s look at ord3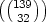 :
:
Well, according to the proposition, we need to look at the digit
sum (base 3) of 139, 32, and 139 - 32 = 107. We have
| 139 |
= (1 . 1) + (1 . 3) + (0 . 32) + (2 . 33) + (1 . 34)
|
| 32 |
= (2 . 1) + (1 . 3) + (0 . 32) + (1 . 33) + (0 . 34) |
| 107 |
= (2 . 1) + (2 . 3) + (2 . 32) + (0 . 33) + (1 . 34) |
So,
| 1393 |
= 12011 |
|
|
| 323 |
= 01012 |
|
|
| 1073 |
= 10222 |
|
|
So,
 3(139) 3(139) |
= 5 |
|
|
 3(32) 3(32) |
= 4 |
|
|
 3(107) 3(107) |
= 7 |
|
|
and proposition 3 says that
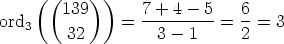 And sure enough,
And sure enough,
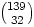 |
= 29794458700044250140618567735660 |
|
= 22 . 33 . 51 . 112 . 171 . 191 . 231 . 371 . 411 . 431 . 591 . 611 . |
|
671 . 1091. 1131 . 1271 . 1311 . 1371 . 1391 |
So, why is  3(32) +
3(32) +  3(107) -
3(107) -  3(139) not 0? If we look at the traditional way we add base-3 numbers (or numbers in any base), we see where
the discrepancy shows up. Here’s how you’d add 32 to 107
to get 139 in base 3:
3(139) not 0? If we look at the traditional way we add base-3 numbers (or numbers in any base), we see where
the discrepancy shows up. Here’s how you’d add 32 to 107
to get 139 in base 3:
| |
|
1 |
1 |
1 |
|
| |
0 |
1 |
0 |
1 |
2 |
| + |
1 |
0 |
2 |
2 |
2 |
|
|
|
|
|
|
| |
1 |
2 |
0 |
1 |
1 |
So, what disturbs the digit sums are the “carries;”
that’s why
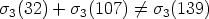 Notice that each carry gets multiplied by 3 when it jumps into
the next column. For example, looking at the rightmost column, the 2 + 2
is 11, so the carried 1 is really 1 . 3 (or 10 in base 3). Let’s look at the general situation:
Notice that each carry gets multiplied by 3 when it jumps into
the next column. For example, looking at the rightmost column, the 2 + 2
is 11, so the carried 1 is really 1 . 3 (or 10 in base 3). Let’s look at the general situation:
Suppose we are looking at 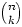 . We write n, k, and n - k in base p:
. We write n, k, and n - k in base p:
| n |
= n0 + n1p + n2p2 + 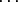 + n sps
+ n sps |
| k |
= k0 + k1p + k2p2 + 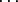 + k sps
+ k sps |
| n - k |
= m0 + m1p + m2p2 + 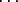 + m sps
+ m sps |
And suppose the carries are denoted by 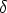 i:
i:
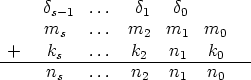 Well, by the way this algorithm works,
Well, by the way this algorithm works,
| m0 + k0 |
= n0 + p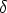 0 0 |
|
|
m1 + k1 + 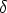 0 0 |
= n1 + p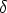 1 1 |
|
|
m2 + k2 + 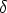 1 1 |
= n2 + p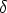 2 2 |
|
|
 |
 |
|
|
ms + ks + 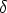 s-1 s-1 |
= ns |
|
|
Then
| m0 + k0 - n0 |
= p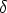 0 0 |
|
|
| m1 + k1 - n1 |
= p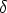 1 - 1 - 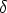 0 0 |
|
|
m2 + k2 - 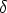 0 0 |
= p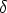 2 - 2 - 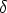 1 1 |
|
|
 |
 |
|
|
| ms + ks - ns |
= -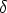 s-1 s-1 |
|
|
Add down:
(m0 + m1 + m2 + 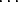 + ms) + (k0 + m1 + k2 +
+ ms) + (k0 + m1 + k2 + 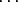 + ks) - (n0 + n1 + n2 +
+ ks) - (n0 + n1 + n2 + 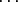 + ns)
+ ns) |
= |
|
|
(p - 1)(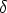 0 + 0 + 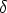 1 + 1 + 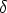 2 + 2 + 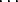 +
+ 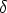 s) s) |
|
|
or
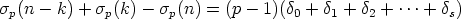 There’s the factor of p - 1. Dividing by it, and combining the result with the result of proposition 3, we have “Kummer’s carry theorem:”
There’s the factor of p - 1. Dividing by it, and combining the result with the result of proposition 3, we have “Kummer’s carry theorem:”
Theorem 1. If n is a non-negative integer and p is a prime,
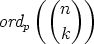 is the number of carries you get when k and n - k are added in base p.
is the number of carries you get when k and n - k are added in base p.
Let’s go back to the original question:
Given a non-negative integer n and a prime p, for how many k is ordp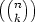 > 0 ?
> 0 ?
In light of theorem 1, this is the same question as:
Given a non-negative integer n and a prime p, for how many k is there a carry when k and n - k are added in base p? Instead of answering this, we found it easier to figure out when
there’s not a carry. And from here, we can subtract (from n + 1) to get the desired answer.
An example will help. Suppose p = 5 and, n = 133866, so, in base 5, n is
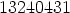 How can two numbers add to this with no carries? Reading from right to left, there are two choices for the first digit—0 and 1. If
k “ends” in 0, n - k ends in 1 and vice-versa. For the “fives” place, there are 4 choices for k—it could have a 0, 1, 2, or 3 in the 5’s place (and n - k would have, respectively, a 3, 2, 1, or 0 in the same place). And so it goes.
Here’s a summary of what can happen:
How can two numbers add to this with no carries? Reading from right to left, there are two choices for the first digit—0 and 1. If
k “ends” in 0, n - k ends in 1 and vice-versa. For the “fives” place, there are 4 choices for k—it could have a 0, 1, 2, or 3 in the 5’s place (and n - k would have, respectively, a 3, 2, 1, or 0 in the same place). And so it goes.
Here’s a summary of what can happen:
| place |
digit in n |
number of choices for digits for k |
| 1 |
1 |
2—namely, {0,1} |
| 5 |
3 |
4—namely, {0,1,2,3} |
| 52 |
4 |
5—namely, {0,1,2,3,4} |
| 53 |
0 |
1—namely, {0} |
| 54 |
4 |
5—namely, {0,1,2,3,4} |
| 55 |
2 |
3—namely, {0,1,2} |
| 56 |
3 |
4—namely, {0,1,2,3 } |
| 57 |
1 |
2—namely, {0,1} |
| |
In general, we have the answer to our question:
Theorem 2. The number of entries in the nth row of Pascal’s triangle that are not divisible by a prime p can be determined as follows:
- Write n in base p:
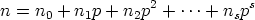
- The number in question is
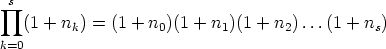
So, for example, suppose p = 2. Then, looking at 100 in base 2:
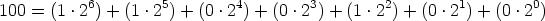 so
so
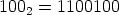 Add 1 to each digit and multiply the answers together:
Add 1 to each digit and multiply the answers together:
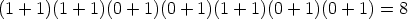 and 8 numbers in the 100th row are not divisible by 2 (that is, are
odd). Try it for 3:
and 8 numbers in the 100th row are not divisible by 2 (that is, are
odd). Try it for 3:
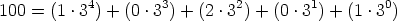 so
so
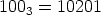 and the number of entries in the 100th row that are not divisible by 3 is
and the number of entries in the 100th row that are not divisible by 3 is
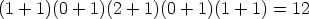 But there are 101 entries in the 100th row, so
101 - 12 = 89 are divisible by 3.
But there are 101 entries in the 100th row, so
101 - 12 = 89 are divisible by 3.
Theorem 1 is due to Ernst Kummer (1810-1893), a mathematician who
laid the groundwork for some of the mathematics that led to the
proof of Fermat’s Last theorem. Indeed, knowing the power of a prime
that divides any particular entry of Pascal’s triangle turns out to be
an essential tool in that proof, and more generally, in all of number theory, so this
project connects to some frontline mathematics.
See Pascal Triangle’s Math Behavior at http://ecademy.agnesscott.edu/~lriddle/ifs/siertri/pascal.htm
for further discussion of the geometric and number theoretic connections
in Pascal’s Triangle.
Results for some Extension Problems
1) Through row 2n-1 – 1, we have 3n-1
odds (this claim comes from the geometric and arithmetic
argument presented above that shows each pattern being copied
twice in subsequent rows). Up through row r, the number
of values overall is
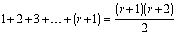 .
.
This expression is the familiar formula for triangular numbers.
So through row 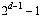 ,
the number of values in the triangle is
,
the number of values in the triangle is
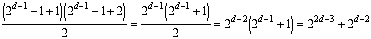 .
.
We can rewrite this expression as
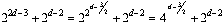 .
.
Therefore, the portion of odds in the triangle through row 2n-1
– 1 is
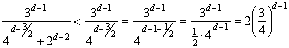 .
.
Since this last expression goes to 0 as d gets larger
and it is an upper bound for the portion of numbers in the triangle
that are odd, the odds represent 0% of the triangle! This surprising
result seems counterintuitive as we look at all of the odd entries
and consider that odds appear in every single row. However, no
matter how small a percent we choose, the percent of odds will
eventually sink below that target.
2) For a discussion of Pascal’s triangle with composite
moduli, see Arithmetic
Properties of Binomial Coefficients at http://www.math.uga.edu/~andrew/Binomial.
See also Granville, Andrew (1992). Zaphod Beeblebrox’s
brain and the fifty-ninth row of Pascal’s triangle. American
Mathematical Monthly, 99: 318-331 and Granville, Andrew (1997).
Corrigendum. American Mathematical Monthly, 104: 848-851.
3) See the Teaching Notes
for a discussion.
4) Have fun!