|
Extension Problems for the Patterns in Pascal’s Triangle Problem
- What is the ratio of the number of odds to the number of evens
in Pascal’s triangle? What does it mean to ask about the
ratio for an infinite object such as this?
- What portion of the triangle is each remainder for a given
modulus (e.g., what portions are 0, 1, or 2 mod 3)?
- Show that
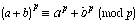for prime p. What does this result tell us about the
distribution of zeroes in Pascal’s triangle mod p?
- Explore “Pascal’s tetrahedron”: a three-dimensional
version of the triangle in which each number is the sum of the
three neighbors above it: PT(l, r,
c) = PT(l – 1, r, c)
+ PT(l – 1, r – 1, c)
+ PT(l – 1, r, c –
1). Can you find settings, parallel to those that generate Pascal’s
triangle, related to this array of numbers?
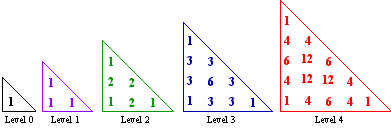
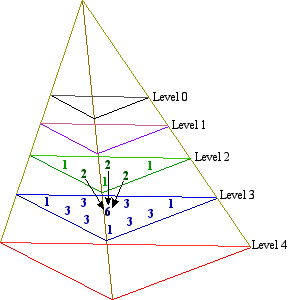
“Pascal’s tetrahedron”
|
|
