Consider the following different definitions:
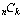 = the number of subsets of size k that can be made
from an n-element set.
= the number of subsets of size k that can be made
from an n-element set.
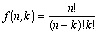
Pascal(n, k) = the entries of Pascal’s
triangle which follow these two rules:
Pascal(n, k) = Pascal(n
– 1, k – 1) + Pascal(n
– 1, k)
Pascal(n, 0) = Pascal(n,
n) = 1.
a) Write out the first few values of 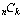 in a triangle:
in a triangle:
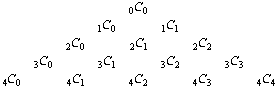
b) Write out the first few values of f(n,
k) in a triangle:
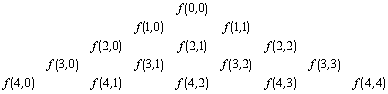
c) Write out the first few values of a Pascal(n,
k) triangle.
d) Show that for any positive integer n and for 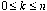 ,
f(n, k) = Pascal(n,
k). Hint: you can do this by showing that f(n,
k) obeys the same rules that define Pascal(n,
k).
,
f(n, k) = Pascal(n,
k). Hint: you can do this by showing that f(n,
k) obeys the same rules that define Pascal(n,
k).
e) Show that for any positive integer n and for 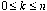 ,
,
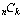 = Pascal(n, k).
= Pascal(n, k).
Because of problems 5d and 5e, we can use the same symbol for
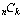 ,
f(n, k), and Pascal(n,
k). By convention, most people use
,
f(n, k), and Pascal(n,
k). By convention, most people use 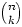 .
.