





 |
Extensions for the Trains Problem
Here are just a few ways you might extend the Trains project:
- How many trains of length n use exactly k cars? For example, think about
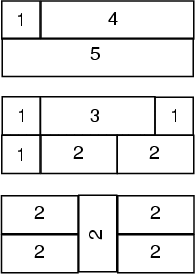
trains of length 5. There is one train that uses only one car: the length 5 car.
There are four trains that use exactly 2 cars: 4-1, 1-4, 2-3, and 3-2. How
many trains use 3, 4, and 5 cars? Now generalize to n and k.
- Suppose you just use cars of length 1 and 2. How does this change the answer
of the total number of trains of length n?
- Lay out all the trains of length 3 on your desk (and nothing else). Here they
are:

You will have on your desk a total of five 1-cars, two 2-cars, and one 3-car.

How many cars (and which ones) will be on your desk if you lay out all the
trains of length 4? Now, clear your desk and lay out all the trains of length 4.
How may cars of each type are on your desk? Generalize to length n.
- Suppose you want to make all the trains of length 3, but not all at the same
time. You want to make them one at a time. How many of each car do you
need? Well, here are the trains:

You need three 1-cars, one 2-car (because any given train only uses one of
them), and one 3-car.

How many cars (and which ones) do you need on your desk to make all
the trains of length 4, doing it one train at a time? Now, suppose you want
to make all the trains of length 5, one at a time. What do you need to add
to the pile on your desk so you can do it? Then how many cars do you need
to add to the pile in order to make all the trains of length 6? Generalize to
length n: How many new cars do you need to add to a pile that lets you make
all trains of length n - 1 in order to get a pile that lets you make all trains of
length n?
- Suppose instead of 1 × n rectangles, your trains were 2 × n rectangles. How
many 2 × n rectangles are there? Here are just some 2 × 5 rectangles.


- Suppose that order doesn’t matter. So the 1-2-2 train is the same as 2-2-1 and
2-1-2. Instead of counting these as three trains, we would only count them
as one. Now how many trains of length n are there? (Warning: this is a very
hard problem!)

|
|