Hints for Pythagorean Triples

In one sense, the answer to the question about the quantity of Pythagorean triples is too simple.  If you start with, for example, 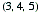, multiplying the numbers by any positive integer k,  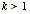, will result in a new Pythagorean triple.

    

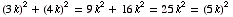
The natural way to restrict Pythagorean triples so that you don't consider multiples like this is to require that the numbers have no common factor.  These are the primitive Pythagorean triples.   Can you find an infinite number of primitive Pythagorean triples?

Once you have a lot of examples, try organizing your data and looking for patterns.

Here's a hint for finding many Pythagorean triples; however you can't find all of them this way.  If you add the first n odd positive integers, you get 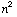.   What if the 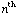odd integer is a perfect square, like 9, 25, or 81?

---