Mathematical Induction

Mathematical induction is a common method for proving theorems about the positive integers, or just about any situation where one case depends on previous cases. Here’s the basic idea, phrased in terms of integers:

You have a conjecture that you think is true for every integer greater than 1. Show (by calculation or some other method) that your conjecture definitely holds for 1.
Show that whenever your conjecture holds for some number, it must hold for the next number as well.

Why does this work? Well, you know your conjecture holds for 1. You’ve shown that whenever it holds for some number, it must hold for the next, so your conjecture also holds for 2. But if it holds for 2, it must hold for the next number as well, so it holds for 3. And so on, through all the integers greater than 1.

A few of things to notice:

The starting point (or base case) of 1 is common, but it’s not the only choice. You might have a conjecture that holds for every integer greater than 5, or for every integer greater than 1,001. The only thing that changes is the base case.
In practice, the way you do Step 2 is that you assume that for some number you call (n-1), your conjecture holds. (This is called the induction hypothesis.) Use that assumption to show that the conjecture must hold for the number n as well. Some people complain that they are “assuming what they want to prove.” That’s not the case, of course. You are simply proving that if your claim is true for a particular case, then it is true for the subsequent one. If no base case can be established, then the link between cases is meaningless. The assumption is no different than the one we make when we say “if a shape is a parallelogram, then its adjacent angles are supplementary.” We have not proven that any shapes are parallelograms. We are just claiming that if a shape exists that matches our definition for parallelogram, that it must also possess the stated property.
A slight variation on the induction hypothesis can be useful: assume that for all integers k < n your conjecture holds. Then use that to prove it holds for the number n as well. If your proof uses more than one previous step--for example, it uses the fact that it holds at (n-1) and (n-2)--you’ll need to check more than one base case.
Mathematical induction and its variations are useful in proving identities that are true for any value of integer, but they do not help you see how someone figured out the identity at first place.
Mathematical induction is not only useful for proving algebraic identities. It can be used any time you have a recursive relationship--one where the current case depends on one or more of the previous cases. See the second example below for a geometric application of induction. Here’s a more general way to think about induction:
1. You have a conjecture that you think is true for every case. Show that your conjecture definitely holds for a base case.
2. Show that whenever your conjecture holds for some case, it must hold for the next case as well.

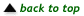
Examples

Here’s an example using integers. Someone discovered a formula that seems to work for the sum of the integers:

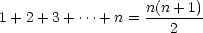
1 + 2+ 3+ ...+ n = n(n+-1)- 2

You could check lots and lots of cases, but no matter how long you worked, you could never check that the formula holds for every integer greater than 1. With mathematical induction, you can prove it does!

Show that the conjecture holds for a base case. Well, the sum on the left will just be 1. The formula on the right gives 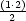= 1. So the formula holds for 1.
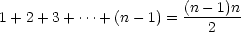
Show that whenever your conjecture holds for some number, it must hold for the next number as well. So, we’ll start with the original formula and show that when it is true for some n - 1, then the formula must also work for n: $(n- 1)n 1+ 2+ 3 + ...+ (n- 1) = ---2----$
Now, the equality will still hold if we add n to both sides of the equation:

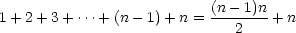
$1 + 2+ 3+ ...+ (n - 1)+ n = (n--1)n+ n 2$
And we do a little simplification on the right side of the equation, trying to get it in the form of our original conjecture:
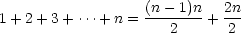
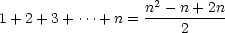
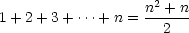
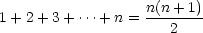
$1+ 2+ 3 +...+ n = (n--1)n-+ 2n- 2 2$ $1+ 2+ 3 +...+ n = n2--n-+-2n 2$ $2 1+ 2 +3 + ...+ n = n--+n- 2$ $n(n + 1) 1+ 2 + 3+ ...+n = -------- 2$
which is exactly our original formula!

So the formula holds for 1. If it holds for 1, it must hold for 2 (the next number). If it holds for 2, it must hold for 3 (the next number). And so on, and so on - by mathematical induction, it holds for every integer greater than 1!

Here’s a geometric example: Someone noticed that every polygon with n sides could be divided into n - 2 triangles. Again, you could never check every polygon, but you don’t have to. Induction lets you prove it. Here’s a sketch of the proof. Can you fill in the details?

In this case, the base case will be quadrilaterals, or polygons with four sides. Draw one diagonal, and you cut it into 2 triangles. (Make sure you believe you can do this for every quadrilateral--sometimes a diagonal will fall outside of the figure. What then?)
Now, assume that for every polygon with n - 1 sides, you can cut them into (n-1)-2 = n-2 triangles. Now think about a polygon with n sides.
- Find a diagonal that creates a triangle and an (n - 1)-sided polygon. (Can you always do this?)
- You can divide the (n-1)-sided polygon into n-3 triangles. (Why?)
- So the total number of triangles is (n - 3) = 1 = n - 2.

Further Resources

You can try your hand at some mathematical induction problems--some numeric and some not--at the Problems with a Point page on The Principle of Mathematical Induction. You can find some harder problems for which induction is useful at http://www.geocities.com/jespinos57/induction.htm.

More information and problems on Mathematical Induction can be found at http://www.math.csusb.edu/notes/proofs/pfnot/node10.html and http://www.cut-the-knot.com/induction.html and in the articles "Teaching Mathematical Induction: An Alternative Approach" and "When Memory Fails" in the September 2001 issue of Mathematics Teacher.