Here are some things to think about:

1. Can you find an interesting set S so that |S_n| is finite but Pr(S) doesn’t exist? Can you find an interesting set S so that |S_n| is bounded but Pr(S) doesn’t exist?
2. What’s the probability that three integers chosen at random are relatively prime? You can do a numerical simulation and even set up an infinite product, but no one knows the exact values for the infinite product you’ll create. It is known that the value is irrational.
3. Learn about the Bernoulli numbers B_n. These are numbers that are defined by the pattern

   B0	= 1
   B0 + 2B1	= 0
   B0 + 3B1 + 3B2	= 0
   B0 + 4B1 + 6B2 + 4B3	= 0

   Yes, these numbers are from Pascal’s triangle. It turns out that 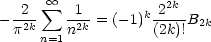This generalizes the formula 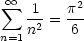to sums of reciprocals of even powers. Do you see how? Very little is known about odd powers.
4. What’s the probability that a prime number will leave a remainder of 3 when you divide it by 4?