These problems all involve picking an integer (or a pair of integers) at random and seeing if it meets a given criterion. Dealing with probability in the integers is hard to think about, because the integers form an infinite set. Well, one way to deal with this is to pick a number at random between 1 and some big number n and see how often it meets the criterion.

Perfect Squares

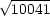
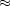
For perfect squares, you can do a direct estimate. For example, how many perfect squares are there between 1 and 10041? Well, every perfect square in this range is the square of an integer between 1 and 100. And, if you pick a number between 1 and 100 and square it, you get a perfect square between 1 and 10041. So, there are 100 perfect squares between 1 and 10041. 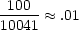So, the probability of a number less than 10041 being a perfect square is Try this reasoning with 10041 replaced by n. Then let n .

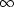
Primes

Now, for the “primality” problem, making this estimate is quite hard. But one way to get a feel for the problem is to try a simulation. For example, you could perform a number of “trials.” In each trial, you can pick a number at random between, say, 1 and 10041. If it’s prime, count it as “good.” Otherwise, don’t count it at all. Do this, say, 1000 times. A good estimate for the probability of a number less than 10041 being prime is the number of good trials divided by 1000.

Of course, you’ll need a computer or calculator for this. Mathematica is especially convenient, because it has a prime-tester PrimeQ built in (actually, all you can conclude if PrimeQ[n] returns True is that there’s a very high probability that n is prime). You can use this to write a function that returns 1 if its input is prime and 0 if it isn’t. Then you can sum this function between 1 and n to get the number of primes less than or equal to n.