This project, more than some of the others, may require you to learn some new
background material. That often happens in research: starting a new problem
requires some prep-time getting to know the territory.
You’ll need to be comfortable with the notion of prime number (we’ll often say
“number” and mean “positive integer”). In later parts of the investigation, you’ll
need to know the fundamental theorem of arithmetic: every number can be factored
in one and only one way into a product of primes. While you don’t need to be able to
prove this, several students who worked on the project took some time out to
understand a proof, and they were glad they did. See The Fundamental Theorem of
Arithmetic for more information.
The project can be approached on both an empirical level, gathering and analyzing
data, and a theoretical level, making a mathematical model and proving
conjectures.
An empirical investigation requires that you know the definition of probability: when
the number of outcomes is finite, it is the number of favorable outcomes divided by
the number of outcomes. It would also help if you are familiar with a software
environment or a programming language that allows you to construct simulations
and test integers for properties like being prime.
In addition, for the theoretical investigation, you’ll need to know about
- limits (facts like
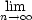
 = 0)
= 0)
- geometric series and other infinite series
- some calculus (integration by parts, integration as area)
- a little trig (addition formulas for sine and cosine)
This sounds formidable, but if you’ve had a good trig course, your teacher or mentor
can bring you up to speed on the rest.